
【題目】拋物線y=﹣x2+bx+c(b,c為常數)與x軸交于點(x1,0)和(x2,0),與y軸交于點A,點E為拋物線頂點.
(Ⅰ)當x1=﹣1,x2=3時,求點E,點A的坐標;
(Ⅱ)①若頂點E在直線y=x上時,用含有b的代數式表示c;
②在①的前提下,當點A的位置最高時,求拋物線的解析式;
(Ⅲ)若x1=﹣1,b>0,當P(1,0)滿足PA+PE值最小時,求b的值.
【答案】(Ⅰ)點A的坐標為(0,3),點E的坐標為(1,4);(Ⅱ)①c=![]() ;②
;②![]() ;(Ⅲ)3+
;(Ⅲ)3+![]() .
.
【解析】
(Ⅰ)根據題意和x1=﹣1,x2=3,可以得到點(﹣1,0),(3,0)在拋物線y=﹣x2+bx+c的圖象上,然后即可求得該拋物線的解析式,再將拋物線解析式化為頂點式,即可得到點A和點E的坐標;
(Ⅱ)①將題目中的函數解析式化為頂點式,再根據題目中頂點E在直線y=x上,即可得到c和b的關系;
②根據①的結果和二次函數的性質,可以求得當點A的位置最高時,拋物線的解析式;
(Ⅲ)根據x1=﹣1,b>0和題目中的函數解析式,可以得到點A的坐標,然后即可求得直線AP的解析式,再根據最短路線問題可以得到當P(1,0)滿足PA+PE值最小時b的值.
解:(Ⅰ)∵拋物線y=﹣x2+bx+c(b,c為常數)與x軸交于點(x1,0)和(x2,0),與y軸交于點A,點E為拋物線頂點,x1=﹣1,x2=3,
∴點(﹣1,0),(3,0)在拋物線y=﹣x2+bx+c的圖象上,
∴![]() ,解得
,解得![]() ,
,
∴y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴點A的坐標為(0,3),點E的坐標為(1,4);
(Ⅱ)①∵y=﹣x2+bx+c=![]() ,
,
∴點E的坐標為(![]() ,
,![]() ),
),
∵頂點E在直線y=x上,
∴![]() =
=![]() ,
,
∴c=![]() ;
;
②由①知,![]() ,
,
則點A的坐標為(0,![]() ),
),
∴當b=1時,此時點A的位置最高,函數y=﹣x2+x+![]() ,
,
即在①的前提下,當點A的位置最高時,拋物線的解析式是![]() ;
;
(Ⅲ)∵x1=﹣1,拋物線y=﹣x2+bx+c過點(x1,0),
∴﹣1﹣b+c=0,
∴c=1+b,
∵點E的坐標為(![]() ,
,![]() ),點A的坐標為(0,c),
),點A的坐標為(0,c),
∴E(![]() ,
,![]() ),A(0,b+1),
),A(0,b+1),
∴點E關于x軸的對稱點E′(![]() ,﹣
,﹣![]() ),
),
設過點A(0,b+1)、P(1,0)的直線解析式為y=kx+t,
![]() ,得
,得![]() ,
,
∴直線AP的解析式為y=(﹣b﹣1)x+(b+1)=﹣(b+1)x+(b+1)=(b+1)(﹣x+1),
∵當直線AP過點E′時,PA+PE值最小,
∴﹣![]() =(b+1)(﹣
=(b+1)(﹣![]() +1),
+1),
化簡得:b2﹣6b﹣8=0,
解得:b1=![]() ,b2=
,b2=![]()
∵b>0,
∴b=![]() ,
,
即b的值是3+![]() .
.


 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,按以下步驟作圖:①以A為圓心,任意長為半徑作弧,分別交AB,AD于點M,N;②分別以M,N為圓心,以大于![]() MN的長為半徑作弧,兩弧相交于點P;③作AP射線,交邊CD于點Q,若DQ=2QC,BC=3,則平行四邊形ABCD周長為________.
MN的長為半徑作弧,兩弧相交于點P;③作AP射線,交邊CD于點Q,若DQ=2QC,BC=3,則平行四邊形ABCD周長為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在三角形![]() 中,
中,![]() ,
,![]() 和
和![]() 關于
關于![]() 對稱
對稱
(1)將圖1中的![]() 以
以![]() 為旋轉中心,逆時針方向旋轉角
為旋轉中心,逆時針方向旋轉角![]() ,使
,使![]() ,得到如圖2所示的
,得到如圖2所示的![]() ,分別延長
,分別延長![]() 和
和![]() 交于點
交于點![]() ,則四邊形
,則四邊形![]() 的形狀是 ;
的形狀是 ;
(2)將圖1中的![]() 以
以![]() 為旋轉中心,按逆時針方向旋轉角
為旋轉中心,按逆時針方向旋轉角![]() ,使
,使![]() ,得到如圖3所示的
,得到如圖3所示的![]() ,連接
,連接![]() 和
和![]() ,得到四邊形
,得到四邊形![]() ,請判斷四邊形
,請判斷四邊形![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)如圖3中,![]() ,將
,將![]() 沿著射線
沿著射線![]() 方向平移
方向平移![]() ,得到
,得到![]() ,連接
,連接![]() ,使四邊形
,使四邊形![]() 恰好為正方形,請直接寫出a的值.
恰好為正方形,請直接寫出a的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔.李明按照相關政策投資銷售本市生產的一種新型節能燈.已知這種節能燈的成本價為每件![]() 元,出廠價為每件
元,出廠價為每件![]() 元,每月銷售量
元,每月銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元)之間的關系近似滿足一次函數:
(元)之間的關系近似滿足一次函數:![]() .
.
(1)李明在開始創業的第一個月將銷售單價定為![]() 元,那么政府這個月為他承擔的總差價為多少元?
元,那么政府這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為![]() (元),當銷售單價定為多少元時,每月可獲得最大利潤?
(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于![]() 元.如果李明想要每月獲得的利潤不低于
元.如果李明想要每月獲得的利潤不低于![]() 元,那么政府為他承擔的總差價最少為多少元?
元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 與直線
與直線![]() 有兩個不同的交點.下列結論:①
有兩個不同的交點.下列結論:①![]() ;②當
;②當![]() 時,
時,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有兩個不等實根;④若連接這兩個交點與拋物線的頂點,恰好是一個等腰直角三角形,則
有兩個不等實根;④若連接這兩個交點與拋物線的頂點,恰好是一個等腰直角三角形,則![]() ;其中正確的結論的個數是( )
;其中正確的結論的個數是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】桃花中學計劃購買![]() 兩種型號的小黑板,經洽談, 購買一塊
兩種型號的小黑板,經洽談, 購買一塊![]() 型小黑板比買一塊
型小黑板比買一塊![]() 型小黑板多
型小黑板多![]() 元,且購買
元,且購買![]() 塊
塊![]() 型小黑板和
型小黑板和![]() 塊
塊![]() 型小黑板共需
型小黑板共需![]() 元.
元.
(1)求購買一塊![]() 型小黑板和一塊
型小黑板和一塊![]() 型小黑板各需要多少元?
型小黑板各需要多少元?
(2)根據學校的實際情況,需購買![]() 兩種型號的小黑板共
兩種型號的小黑板共![]() 塊,并且購買
塊,并且購買![]() 型小黑板的數量不少于購買
型小黑板的數量不少于購買![]() 型小黑板的數量,請問學校購買這批小黑板最少要多少元?
型小黑板的數量,請問學校購買這批小黑板最少要多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年中國北京世界園藝博覽會已于2019年4月29日在北京市延慶區開展,吸引了大批游客參觀游覽.五一小長假期間平均每天入園人數大約是8萬人,佳佳等5名同學組成的學習小組,隨機調查了五一假期中入園參觀的部分游客,獲得了他們在園內參觀所用時間,并對數據進行整理,描述和分析,下面給出了部分信息:
a.參觀時間的頻數分布表如下:
時間 | 頻數(人數) | 頻率 |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
合計 |
| 1.000 |
b.參觀時間的頻數分布直方圖如圖:
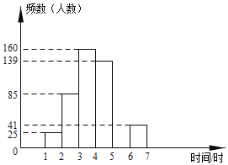
根據以上圖表提供的信息,解答下列問題:
(1)這里采用的調查方式是 ;
(2)表中![]() ,
,![]() ,
,![]() ;
;
(3)并請補全頻數分布直方圖;
(4)請你估算五一假期中平均每天參觀時間小于4小時的游客約有多少萬人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:點![]() 和
和![]() 是一次函數
是一次函數![]() 與反比例函數
與反比例函數![]() 圖象的兩個不同交點,點
圖象的兩個不同交點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,直線
,直線![]() 以及
以及![]() 分別與
分別與![]() 軸交與點
軸交與點![]() 和點
和點![]() .
.
(1)求反比例函數![]() 的表達式;
的表達式;
(2)若![]() ,求
,求![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設函數y=k1x+![]() ,且k1k2≠0,自變量x與函數值y滿足以下表格:
,且k1k2≠0,自變量x與函數值y滿足以下表格:
x | …… | -4 | -3 | -2 | -1 | - |
| 1 | 2 | 3 | 4 | …… |
y | …… | -3 | -2 | -1 | 0 | 1 | -1 | 0 | 1 | m | n | …… |
(1)根據表格直接寫出y與x的函數表達式及自變量x的取值范圍______
(2)補全上面表格:m=______,n=______;在如圖所示的平面直角坐標系中,請根據表格中的數據補全y關于x的函數圖象;
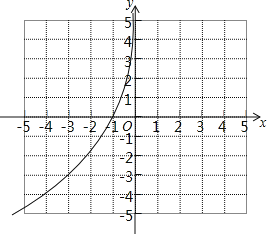
(3)結合函數圖象,解決下列問題:
①寫出函數y的一條性質:______;
②當函數值y≥![]() 時,x的取值范圍是______;
時,x的取值范圍是______;
③當函數值y=-x時,結合圖象請估算x的值為______(結果保留一位小數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com