

分析 先連接EC、EE′,設EE′交AD于N,根據正方形的性質以及折疊的性質,求出NE、ND的長,以及正方形ABCD的對角線長和邊長,再根據CF是△ACE的中線,求出△ACF的面積,根據E′F是△AE′E的中線,求出△AE′F的面積,最后根據四邊形CDE′F的面積=S梯形ACDE′-S△ACF-S△AE′F進行計算,即可解決問題.
解答 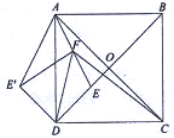 解:連接EE′,交AD于N,連接CE,
解:連接EE′,交AD于N,連接CE,
在正方形ABCD中,∠EDN=45°,
由折疊得,AD垂直平分EE′,且∠EDN=∠E′DN=45°,DE=DE′,
∴△DEE′、△DEN、△DE′N均為等腰直角三角形,
∵DE=2$\sqrt{2}$,$\frac{OE}{DE}$=$\frac{1}{2}$,
∴OE=$\sqrt{2}$,DN=EN=E′N=2,DO=3$\sqrt{2}$,DE′=2$\sqrt{2}$,
∴AC=6$\sqrt{2}$,AD=6,
∵EO⊥AC,
∴S△ACE=$\frac{1}{2}$×6$\sqrt{2}$×$\sqrt{2}$=6,
又∵點F是AE的中點,
∴S△ACF=$\frac{1}{2}$×S△ACE=3,
∵AN⊥EE′,AN=AD-DN=6-2=4,
∴S△AE′E=$\frac{1}{2}$×4×4=8,
又∵點F是AE的中點,
∴S△AE′F=$\frac{1}{2}$×S△AE′E=4,
∵∠E′DO=∠AOD=90°,
∴DE′∥AC,
∴S梯形ACDE′=$\frac{(DE′+AC)×DO}{2}$=$\frac{(2\sqrt{2}+6\sqrt{2})×3\sqrt{2}}{2}$=24,
∴四邊形CDE′F的面積=S梯形ACDE′-S△ACF-S△AE′F=24-3-4=17.
故答案為:17
點評 本題以折疊問題為背景,主要考查了正方形的性質、等腰直角三角形的性質以及中線的性質的綜合運用,難度較大.折疊是一種軸對稱變換,折疊前后圖形的形狀和大小不變,對應邊相等,對應角相等.解題的關鍵是添加輔助線,運用割補法求四邊形的面積.


科目:初中數學 來源: 題型:選擇題
 如圖,如果將△ABC的頂點A向左平移3個單位后再向下平移一個單位到達A′點,連接A′C,那么線段A′C與線段AB的位置關系是( )
如圖,如果將△ABC的頂點A向左平移3個單位后再向下平移一個單位到達A′點,連接A′C,那么線段A′C與線段AB的位置關系是( )| A. | 相等 | B. | 相交 | C. | 垂直 | D. | 平行 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,將直角坐標系中“魚”的圖案關于x軸翻折,那么點A的對應點A′的坐標是( )
如圖,將直角坐標系中“魚”的圖案關于x軸翻折,那么點A的對應點A′的坐標是( )| A. | (-5,4) | B. | (4,-2) | C. | (5,-2) | D. | (5,-4). |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| x | 3000 | 4000 | 5000 | 6000 |
| y1 | 37000 | 85000 | ||
| y2 | 51000 | 68000 | 102000 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
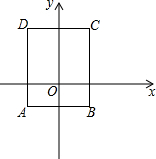 如圖,四邊形ABCD是長方形,AB=3,AD=4.已知A(-$\frac{3}{2}$,-1),則點C的坐標是( )
如圖,四邊形ABCD是長方形,AB=3,AD=4.已知A(-$\frac{3}{2}$,-1),則點C的坐標是( )| A. | (-3,$\frac{3}{2}$) | B. | ($\frac{3}{2}$,-3) | C. | (3,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,3) |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2a3b=a2•2ab | B. | (x+3)(x-3)=x2-9 | ||
| C. | 2x2+4x-3=2x(x+2)-3 | D. | ax+ay=a(x+y) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com