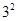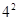觀察下列各式,并回答問題
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
…
(1)請你寫出第10個式子;
(2)請你用含 n 的式子表示上述式子所表述的規律;
(3)計算1+3+5+7+9…+1003+1005+…+2009+2011;
(4)計算:1005+1007+…+2009+2011.
解:(1)1+3+5+7+9+11+13+15+17+19+21=121=112;
(2)1+3+5+7+9+…+2n+1=(n+1)2;
(3)1+3+5+7+9…+1003+1005+…+2009+2011=10062;
(4)原式=10062-5022=760032.
分析:(1)由1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,…可以看出連續奇數的和等于數的個數的平方;由此可以寫出第10個式子;
(2)自然數n(n≥1)表示奇數為2n+1,因此得到一般規律;
(3)根據(2)中的規律可直接計算出結果;
(4)1005+1007+…+2009+2011=(1+3+5+…+2011)-(1+3+5+…+1003),再用(2)中的規律計算即可.
點評:此題主要考查了數字的變化規律,探尋數列規律:認真觀察、仔細思考,善用聯想是解決這類問題的方法.