
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=3,AB=5.點P從點A出發,以每秒5個單位
長度的速度沿AC方向運動,過點P作PQ⊥AB于點Q,當點Q和點B重合時,點P停止運動,以AP和AQ為邊作APHQ.設點P的運動時間為t秒(t>0)
(1)線段PQ的長為 .(用含t的代數式表示)
(2)當點H落在邊BC上時,求t的值.
(3)當APHQ與△ABC的重疊部分圖形為四邊形時,設四邊形的面積為S,求S與t之間的函數關系式.
(4)過點C作直線CD⊥AB于點D,當直線CD將APHQ分成兩部分圖形的面積比為1:7時,直接寫出t的值.

【答案】(1)4t;(2)t=![]() ;(3)當0<t≤
;(3)當0<t≤![]() 時, S=12t2,當
時, S=12t2,當![]() ≤t≤
≤t≤![]() 時,S==﹣
時,S==﹣![]() t2+
t2+![]() t;(4)t的值為
t;(4)t的值為![]() 或
或![]() s.
s.
【解析】
(1)利用勾股定理求出BC,再根據sinA=![]() ,構建方程即可解決問題;
,構建方程即可解決問題;
(2)如圖2中,因為QH∥AC,可得![]() ,由此構建方程即可解決問題;
,由此構建方程即可解決問題;
(3)兩種情形分別求解:①如圖3中,當0<t≤![]() 時,重疊部分是四邊形APHQ.②如圖4中,當
時,重疊部分是四邊形APHQ.②如圖4中,當![]() ≤t≤
≤t≤![]() 時,重疊部分是四邊形ACMQ;
時,重疊部分是四邊形ACMQ;
(4)兩種情形畫出圖形分別利用三角形的中位線定理求解即可;
(1)如圖1中,
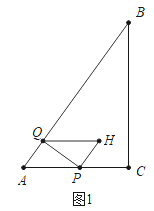
在Rt△ACB中,∵AC=3,AB=5,∠C=90°,
∴BC=![]() =4,
=4,
∵AP=5t,sinA=![]() ,
,
∴![]() ,
,
∴PQ=4t,AQ=![]() =3t.
=3t.
故答案為4t.
(2)如圖2中,當點H落在BC上時.
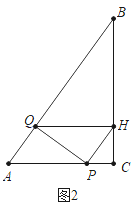
∵QH∥AC,
∴![]() ,
,
∴![]() ,
,
∴t=![]() .
.
(3)①如圖3中,當0<t≤![]() 時,重疊部分是四邊形APHQ.S=12t2.
時,重疊部分是四邊形APHQ.S=12t2.

②如圖4中,當![]() ≤t≤
≤t≤![]() 時,重疊部分是四邊形ACMQ,
時,重疊部分是四邊形ACMQ,
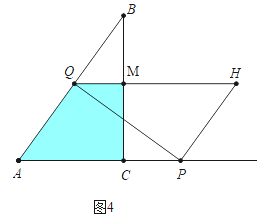
S=![]() =﹣
=﹣![]() t2+
t2+![]() t.
t.
(4)①如圖5中,∵S△HEF:S五邊形EQAPF=1:7,CD∥PQ,
∴EF是△HPQ的中位線.
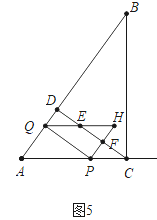
∵cos∠A=![]() ,
,
∴AD=![]() ,
,
∵QH∥AC,
∴∠DQE=∠A,
∴cos∠DQE=cos∠A=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴t=![]() .
.
②如圖6中,當S△ADC:S五邊形CDQHP=1:7時,CD是△APQ的中位線.
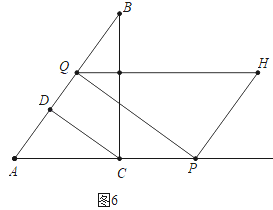
∴AQ=2AD,
∴3t=2×![]() ,
,
∴t=![]() .
.
綜上所述,滿足條件的t的值為![]() 或
或![]() s.
s.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某地地震牽動著全國人民的心,某單位開展了“一方有難,八方支援”賑災捐款活動.第一天收到捐款![]() 元,第三天收到捐款
元,第三天收到捐款![]() 元.
元.
![]() 如果第二天、第三天收到捐款的增長率相同,求捐款增長率?
如果第二天、第三天收到捐款的增長率相同,求捐款增長率?
![]() 按照
按照![]() 中收到捐款的增長率不變,該單位三天一共能收到多少捐款?
中收到捐款的增長率不變,該單位三天一共能收到多少捐款?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC為等邊三角形,E為射線BA上一點,D為直線BC上一點,ED=EC.
(1)當點E在AB的上,點D在CB的延長線上時(如圖1),求證:AE+AC=CD;
(2)當點E在BA的延長線上,點D在BC上時(如圖2),猜想AE、AC和CD的數量關系,并證明你的猜想;
(3)當點E在BA的延長線上,點D在BC的延長線上時(如圖3),請直接寫出AE、AC和CD的數量關系.
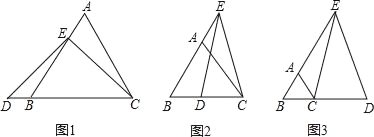
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=110°,點E、G分別是AB、AC的中點,DE⊥AB交BC于D,FG⊥AC交BC于F,連接AD、AF.試求∠DAF的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某建筑工程隊利用一面墻(墻的長度不限),用40米長的籬笆圍成一個長方形的倉庫.
(1)求長方形的面積是150平方米,求出長方形兩鄰邊的長;
(2)能否圍成面積220平方米的長方形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年初,“合肥百大”商場在濱湖新區隆重開業,某服裝經銷商發現某款新型運動服市場需求較大,該服裝的進價為![]() 元/件,每年支付員工工資和場地租金等其它費用總計
元/件,每年支付員工工資和場地租金等其它費用總計![]() 元.經過市場調查發現如果銷售單價為
元.經過市場調查發現如果銷售單價為![]() 元/件,則年銷售量為
元/件,則年銷售量為![]() 件.
件.
![]() 用含
用含![]() 的代數式表示年獲利金額
的代數式表示年獲利金額![]() ;
;
注:年獲利![]() (銷售單價-進價)
(銷售單價-進價)![]() 年銷售量-其它費用
年銷售量-其它費用
![]() 若經銷商希望該服裝一年的銷售獲利達
若經銷商希望該服裝一年的銷售獲利達![]() 元,且要使產品銷售量較大,你認為銷售單價應定為多少元?
元,且要使產品銷售量較大,你認為銷售單價應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D是△ABC外接圓上的動點,且B,D位于AC的兩側,DE⊥AB,垂足為E,DE的延長線交此圓于點F.BG⊥AD,垂足為G,BG交DE于點H,DC,FB的延長線交于點P,且PC=PB.
(1)求證:BG∥CD;
(2)設△ABC外接圓的圓心為O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
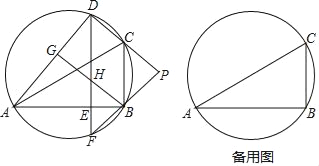
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com