


 智慧小復習系列答案
智慧小復習系列答案科目:初中數學 來源: 題型:單選題
| 袋號 | 一 | 二 | 三 | 四 |
| 質量/kg | 10.2 | 9.7 | 9.9 | 9.6 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
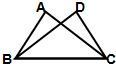 如圖,∠ABC=∠DCB,需要補充一個直接條件才能使△ABC≌△DCB、甲、乙、丙、丁四位同學填寫的條件分別是:甲“AB=DC”;乙“AC=DB”;丙“∠A=∠D”;丁“∠ACB=∠DBC”.那么這四位同學填寫錯誤的是________.
如圖,∠ABC=∠DCB,需要補充一個直接條件才能使△ABC≌△DCB、甲、乙、丙、丁四位同學填寫的條件分別是:甲“AB=DC”;乙“AC=DB”;丙“∠A=∠D”;丁“∠ACB=∠DBC”.那么這四位同學填寫錯誤的是________.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com