
【題目】(1)解下列方程.
①![]() 根為______;
根為______;
②![]() 根為______;
根為______;
③![]() 根為______;
根為______;
(2)根據這類方程特征,寫出第n個方程和它的根;
(3)請利用(2)的結論,求關于x的方程![]() (n為正整數)的根.
(n為正整數)的根.
【答案】(1)①![]() ;②
;②![]() ;③
;③![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)首先去分母,即可化成一元二次方程,解方程求得![]() 的值,然后進行檢驗,即可求得方程的解;
的值,然后進行檢驗,即可求得方程的解;
(2)根據(1)中的三個方程的規律特點以及解的關系即可求解;
(3)根據(2)的結果,把所求的方程化成![]() 的形式,把
的形式,把![]() 當作一個整體即可求解.
當作一個整體即可求解.
解:(1)①去分母,得:![]() ,即
,即![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
經檢驗:![]() ,
,![]() 都是方程的解,
都是方程的解,
所以原分式方程的解是![]() ,
,![]() ;
;
②去分母,得:![]() ,即
,即![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
經檢驗:![]() ,
,![]() 是方程的解,
是方程的解,
所以原分式方程的解是![]() ,
,![]() ;
;
③去分母,得:![]() ,即
,即![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,
經檢驗![]() ,
,![]() 是方程的解,
是方程的解,
所以原分式方程的解是![]() ,
,![]() ;
;
(2)根據(1)中的規律可以寫出第![]() 個方程為
個方程為![]() ,
,
去分母,得![]() ,即:
,即:![]() ,
,
則:![]() ,解是
,解是![]() ,
,![]() ;
;
經檢驗:![]() ,
,![]() 是方程的解,
是方程的解,
所以原分式方程的解是![]() ,
,![]() ;
;
(3)![]() ,
,
即![]() ,
,
設![]() ,則原方程變為:
,則原方程變為:![]() ,
,
利用(2)中的結論可知:![]() ,
,
即:![]() 或
或![]() ,
,
解得:![]() ,
,
經檢驗:![]() 是方程的解,
是方程的解,
所以原分式方程的解是![]() .
.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 的中點,在邊
的中點,在邊![]() 上取點
上取點![]()
![]() ,點
,點![]() 在邊
在邊![]() 上,且滿足
上,且滿足![]() ,連接
,連接![]() ,作
,作![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,線段
,線段![]() ,
,![]() ,
,![]() 將
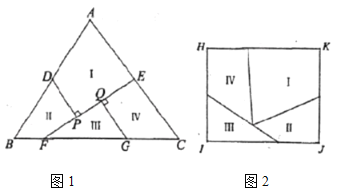
將![]() 分割成I、II、III、IV四個部分,將這四個部分重新拼接可以得到如圖2所示的矩形
分割成I、II、III、IV四個部分,將這四個部分重新拼接可以得到如圖2所示的矩形![]() ,若
,若![]() ,則圖1中
,則圖1中![]() 的長為_______.
的長為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①所示,在△ABC中,點O是AC上一點,過點O的直線與AB,BC的延長線分別相交于點M,N.
【問題引入】
(1)若點O是AC的中點, ![]() ,求
,求![]() 的值;
的值;
溫馨提示:過點A作MN的平行線交BN的延長線于點G.
【探索研究】
(2)若點O是AC上任意一點(不與A,C重合),求證: ![]() ;
;
【拓展應用】
(3)如圖②所示,點P是△ABC內任意一點,射線AP,BP,CP分別交BC,AC,AB于點D,E,F.若![]() ,
, ![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
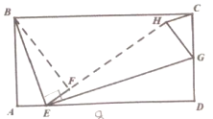
【題目】如圖,矩形ABCD中,AB=4,AD=8,點E為AD上一點,將△ABE沿BE折疊得到△FBE,點G為CD上一點,將△DEG沿EG折疊得到△HEG,且E、F、H三點共線,當△CGH為直角三角形時,AE的長為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
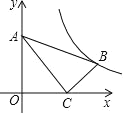
【題目】如圖,在平面直角坐標系中,Rt△ABC的頂點A.C的坐標分別是(0,3)、(4,0).∠ACB=90,AC=2BC,則函數y=![]() (k>0,x>0)的圖象經過點B,則k的值為( )
(k>0,x>0)的圖象經過點B,則k的值為( )
A.10B.11C.12D.13
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC中,D是BC的中點,點G在AD上(點G不與A重合),過點G的直線交AB于E,交射線AC于點F,設AE=xAB,AF=yAC(x,y≠0).
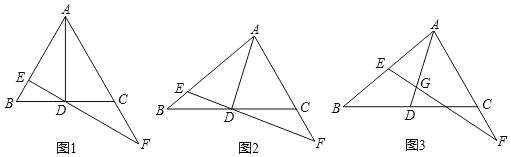
(1)如圖1,若△ABC為等邊三角形,點G與D重合,∠BDE=30,求證:△AEF∽△DEA;
(2)如圖2,若點G與D重合,求證:x+y=2xy;
(3)如圖3,若AG=nGD,x=![]() ,y=
,y=![]() ,直接寫出n的值.
,直接寫出n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
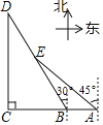
【題目】如圖為某景區五個景點A,B,C,D,E的平面示意圖,B,A在C的正東方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000![]() m,E在BD的中點處.
m,E在BD的中點處.
(1)求景點B,E之間的距離;
(2)求景點B,A之間的距離.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為阻斷新冠疫情向校園蔓延,確保師生生命安全和身體健康,教育部通知,2020年春季學期延期開學,利用網上平臺,停課不停學”,某校對初三全體學生數學線上學習情況進行調查,隨機抽取部分學生的4月月診斷性測試成績,按由高到低分為A,B,C,D四個等級,根據調查的數據繪制成如下的條形統計圖和扇形統計圖,請根據圖中的信息,解答下列問題:
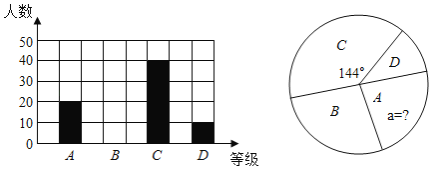
(1)該校共抽查了 名同學的數學測試成績,扇形統計圖中A等級所占的百分比a= ;
(2)補全條形統計圖;
(3)若該校初三共有1180名同學,請估計該校初三學生數學測試成績優秀(測試成績B級以上為優秀,含B級)約有 名;
(4)該校老師想從兩男、兩女四位學生中隨機選擇兩位了解平時線上學習情況,請用列表或畫樹形圖的方法求出恰好選中一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 經過
經過![]() ,
,![]() 兩點,與x軸的另一個交點為C,頂點為D,連結CD.
兩點,與x軸的另一個交點為C,頂點為D,連結CD.
(1)求該拋物線的表達式;
(2)點P為該拋物線上一動點(與點B、C不重合),設點P的橫坐標為t.
①當點P在直線BC的下方運動時,求![]() 的面積的最大值;
的面積的最大值;
②該拋物線上是否存在點P,使得![]() 若存在,求出所有點P的坐標;若不存在,請說明理由.
若存在,求出所有點P的坐標;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com