
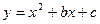 的圖象與y軸交于點A(0,-6),與x軸的一個交點坐標是B(-2,0).
的圖象與y軸交于點A(0,-6),與x軸的一個交點坐標是B(-2,0). 個單位長度,求所得圖象對應的函數關系式.
個單位長度,求所得圖象對應的函數關系式. 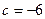 ···························································(1分)
···························································(1分)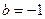 ··························································(2分)
··························································(2分) ················································································(3分)
················································································(3分)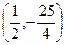 ····························································································(4分)
····························································································(4分) 個單位長度得:
個單位長度得: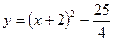 ··············(6分)解析:
··············(6分)解析:

科目:初中數學 來源: 題型:
(本小題滿分10分)已知二次函數![]()
(1)當![]() 時,函數值
時,函數值![]() 隨
隨![]() 的增大而減小,求
的增大而減小,求![]() 的取值范圍。
的取值范圍。
(2)以拋物線![]() 的頂點
的頂點![]() 為一個頂點作該拋物線的內接正三角形
為一個頂點作該拋物線的內接正三角形![]() (
(![]() ,
,![]() 兩點在拋物線上),請問:△
兩點在拋物線上),請問:△![]() 的面積是與
的面積是與![]() 無關的定值嗎?若是,請求出這個定值;若不是,請說明理由。
無關的定值嗎?若是,請求出這個定值;若不是,請說明理由。
(3)若拋物線![]() 與
與![]() 軸交點的橫坐標均為整數,求整數
軸交點的橫坐標均為整數,求整數![]() 的值。
的值。
查看答案和解析>>
科目:初中數學 來源: 題型:

 時,函數值
時,函數值 隨
隨 的增大而減小,求
的增大而減小,求 的取值范圍。
的取值范圍。 的頂點
的頂點 為一個頂點作該拋物線的內接正三角形
為一個頂點作該拋物線的內接正三角形 (
( ,
,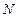 兩點在拋物線上),請問:△
兩點在拋物線上),請問:△ 的面積是與
的面積是與 無關的定值嗎?若是,請求出這個定值;若不是,請說明理由。
無關的定值嗎?若是,請求出這個定值;若不是,請說明理由。 與
與 軸交點的橫坐標均為整數,求整數
軸交點的橫坐標均為整數,求整數 的值。
的值。
查看答案和解析>>
科目:初中數學 來源:2012屆浙江省新昌縣實驗中學九年級上學期期中階段性測試數學卷 題型:解答題
(本題12分)已知二次函數的圖象經過點(0,-3),且頂點坐標為(-1,-4).
(1)求該二次函數的解析式;
(2)設該二次函數的圖象與x軸的交點為A、B,與y軸的交點為C,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源:2013屆浙江建德李家鎮初級中學九年級上學期期末考試數學試卷(帶解析) 題型:解答題
(本題8分)已知二次函數 。
。
(1)求函數圖象的頂點坐標、對稱軸及與坐標軸交點的坐標;
(2)并畫出函數的大致圖象,并求使y>0的x的取值范圍。
查看答案和解析>>
科目:初中數學 來源:2011年初中畢業升學考試(廣西欽州卷)數學 題型:解答題
(本題滿分10分)已知二次函數 的圖象與x軸分別交于點A、B,與y軸交于點C.點D是拋物線的頂點.
的圖象與x軸分別交于點A、B,與y軸交于點C.點D是拋物線的頂點.
(1)如圖①,連接AC,將△OAC沿直線AC翻折,若點O的對應點O'恰好落在該拋物
線的對稱軸上,求實數a的值;
(2)如圖②,在正方形EFGH中,點E、F的坐標分別是(4,4)、(4,3),邊HG位于
邊EF的右側.小林同學經過探索后發現了一個正確的命題:“若點P是邊EH或邊HG上的
任意一點,則四條線段PA、PB、PC、PD不能與任何一個平行四邊形的四條邊對應相等(即
這四條線段不能構成平行四邊形).”若點P是邊EF或邊FG上的任意一點,剛才的結論是
否也成立?請你積極探索,并寫出探索過程;
(3)如圖②,當點P在拋物線對稱軸上時,設點P的縱坐標t是大于3的常數,試問:是
否存在一個正數a,使得四條線段PA、PB、PC、PD與一個平行四邊形的四條邊對應相等
(即這四條線段能構成平行四邊形)?請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com