
【題目】![]() 中,
中,![]() ,點
,點![]() 是邊
是邊![]() 上不與點
上不與點![]() 重合的一點,作
重合的一點,作![]() 交邊
交邊![]() 于
于![]() 點.
點.
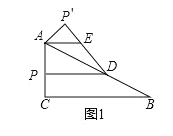
![]() 如圖1,將
如圖1,將![]() 沿直線
沿直線![]() 翻折,得到
翻折,得到![]() ,作
,作![]() .求證:
.求證:![]() ;
;
![]() 將
將![]() 繞點
繞點![]() 順時針旋轉,得到
順時針旋轉,得到![]() ,點
,點![]() 的對應點分別為點
的對應點分別為點![]()
①如圖2,當點![]() 在
在![]() 內部時,連接
內部時,連接![]() 和
和![]() ,求證:
,求證:![]() ;
;
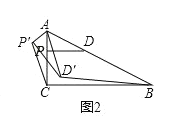
②如果![]() 連接
連接![]() 且
且![]() 那么請直接寫出點
那么請直接寫出點![]() 到直線
到直線![]() 的距離.
的距離.
【答案】(1)詳見解析;(2)①詳見解析;②點![]() 到直線
到直線![]() 的距離為
的距離為![]() 或
或![]()
【解析】
(1)由折疊的性質和平行線的性質可得∠EAD=∠ADP=∠ADP',即可得AE=DE;
(2)①由題意可證△APD∽△ACB,可得![]() ,由旋轉的性質可得AP=AP',AD=AD',∠PAD=∠P'AD',即∠P'AC=∠D'AB,
,由旋轉的性質可得AP=AP',AD=AD',∠PAD=∠P'AD',即∠P'AC=∠D'AB,![]() ,則△AP'C∽△AD'B;
,則△AP'C∽△AD'B;
②分點D'在直線BC的下方和點D'在直線BC的上方兩種情況討論,根據平行線分線段成比例,可求PD=![]() ,通過證明△AMD'≌△DPA,可得AM=PD=
,通過證明△AMD'≌△DPA,可得AM=PD=![]() ,即可求點D'到直線BC的距離.
,即可求點D'到直線BC的距離.
![]() 證明:
證明:![]() 將
將![]() 沿直線
沿直線![]() 翻折,得到
翻折,得到![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]() 旋轉,
旋轉,
![]() ,
,
![]() ,
,![]()
![]()
![]() 若點
若點![]() 在直線
在直線![]() 下方,如圖,過點
下方,如圖,過點![]() 作
作![]() ,過點
,過點![]() 作
作![]() 交
交![]() 的延長線于
的延長線于![]()

![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]() 旋轉,
旋轉,
![]() ,且
,且![]()
![]() ,
,![]() ,
,
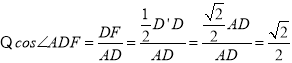
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,且
,且![]()
![]()
![]()
![]() ,
,
![]()
![]() 點
點![]() 到直線
到直線![]() 的距離為
的距離為![]()
若點![]() 在直線
在直線![]() 的上方,如圖,過點
的上方,如圖,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,
,
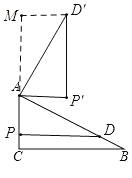
同理可證:![]() ,
,
![]()
![]()
![]()
![]() 點
點![]() 到直線
到直線![]() 的距離為
的距離為![]()
綜上所述:點![]() 到直線
到直線![]() 的距離為
的距離為![]() 或
或![]() .
.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案科目:初中數學 來源: 題型:
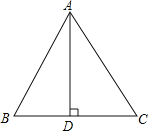
【題目】如圖,在等邊△ABC中,AB=6,AD是高.
(1)尺規作圖:作△ABC的外接圓⊙O(保留作圖痕跡,不寫作法)
(2)在(1)所作的圖中,求線段AD,BD與弧![]() 所圍成的封閉圖形的面積.
所圍成的封閉圖形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
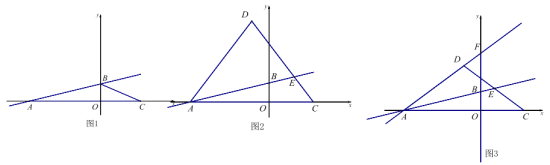
【題目】已知,如圖,在平面直角坐標系中,直線AB:![]() 交x軸于點A(-4,0),交y軸于點B,點C(2,0).
交x軸于點A(-4,0),交y軸于點B,點C(2,0).
(1)如圖1,求直線AB的解析式;
(2)如圖2,點D為第二象限內一點,且AD=DC,DC交直線AB于點E,設DE:EC=m,點D的縱坐標為d,求d與m的函數關系式(不要求寫出自變量的取值范圍);
(3)如圖3,在(2)的條件下,直線AD交y軸于點F,點P為線段AF上一點,G為y軸負半軸上一點,PG=AB,且∠PGF+∠BAF=∠AFB,當m=1時,求點G的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商家今年3月份兩次同時購進了甲、乙兩種不同單價的糖果,第一次購買甲種糖果的數量比乙種糖果的數量多50%,第二次購買甲種糖果的數量比第一次購買甲種糖果的數量少60%,結果第二次購買糖果的總數量雖然比第一次購買糖果的總數量多20%,但第二次購買甲乙糖果的總費用卻比第一次購買甲乙糖果的總費用費少10%.(甲,乙兩種糖果的單價不變),則乙種糖果的單價是甲種糖果單價的_____%.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市促銷活動,將A,B,C三種水果采用甲、乙、丙三種方式搭配裝進禮盒進行銷售.每盒的總成本為盒中A,B,C三種水果成本之和,盒子成本忽略不計.甲種方式每盒分別裝A,B,C三種水果6kg,3kg,1kg;乙種方式每盒分別裝A,B,C三種水果2kg,6kg,2kg.甲每盒的總成本是每千克A水果成本的12.5倍,每盒甲的銷售利潤率為20%;每盒甲比每盒乙的售價低25%;每盒丙在成本上提高40%標價后打八折出售,獲利為每千克A水果成本的1.2倍.當銷售甲、乙、丙三種方式搭配的禮盒數量之比為2:2:5時,則銷售總利潤率為_____.(利潤率=利潤÷成本×100%)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為3cm,動點M從點B出發以3cm/s的速度沿著邊BC﹣CD﹣DA運動,到達點A停止運動,另一動點N同時從點B出發,以1cm/s的速度沿著邊BA向點A運動,到達點A停止運動,設點M運動時間為x(s),△AMN的面積為y(cm2),則y關于x的函數圖象是( )

A. 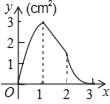 B.
B. 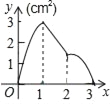 C.
C. 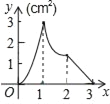 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AB=8.
(1)作△ABC的內角∠CAB的平分線,與邊BC交于點D(用尺規作圖,保留作圖痕跡,不要求寫作法);
(2)若AD=BD,求CD的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是![]() 上一動點,連接AP,作∠APC=45°,交弦AB于點C.AB=6cm.
上一動點,連接AP,作∠APC=45°,交弦AB于點C.AB=6cm.

小元根據學習函數的經驗,分別對線段AP,PC,AC的長度進行了測量.
下面是小元的探究過程,請補充完整:
(1)下表是點P是![]() 上的不同位置,畫圖、測量,得到線段AP,PC,AC長度的幾組值,如下表:
上的不同位置,畫圖、測量,得到線段AP,PC,AC長度的幾組值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①經測量m的值是 (保留一位小數).
②在AP,PC,AC的長度這三個量中,確定![]() 的長度是自變量,
的長度是自變量,![]() 的長度和 的長度都是這個自變量的函數;
的長度和 的長度都是這個自變量的函數;
(2)在同一平面直角坐標系xOy中,畫出(1)中所確定的函數圖象;

(3)結合函數圖象,解決問題:當△ACP為等腰三角形時,AP的長度約為 cm(保留一位小數).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com