【題目】如圖，直線AB與x軸交于點A（1，0），與y軸交于點B（0，﹣2）． 
（1）求直線AB的解析式；
（2）若直線AB上的點C在第一象限，且S△BOC=2，求經過點C的反比例函數的解析式．
【答案】
（1）解：設直線AB的解析式為y=kx+b（k≠0），
∵直線AB過點A（1，0）、點B（0，﹣2），
∴ 
，解得 
，
∴直線AB的解析式為y=2x﹣2
（2）解：設點C的坐標為（m，n），經過點C的反比例函數的解析式為y= 
，
∵點C在第一象限，
∴S△BOC= 
×2×m=2，
解得：m=2，
∴n=2×2﹣2=2，
∴點C的坐標為（2，2），
則a=2×2=4，
∴經過點C的反比例函數的解析式為y= 
【解析】（1）設直線AB的解析式為y=kx+b，將點A（1，0）、點B（0，﹣2）分別代入解析式即可組成方程組，從而得到AB的解析式；（2）根據三角形的面積公式和直線解析式求出點C的坐標，即可求解．
云南師大附小一線名師提優作業系列答案科目：初中數學 來源： 題型：
【題目】閱讀下面材料： 如圖1，在平面直角坐標系xOy中，直線y1=ax+b與雙曲線y2= 
交于A（1，3）和B（﹣3，﹣1）兩點．
觀察圖象可知：
①當x=﹣3或1時，y1=y2；
②當﹣3＜x＜0或x＞1時，y1＞y2 ， 即通過觀察函數的圖象，可以得到不等式ax+b＞ 的解集．
有這樣一個問題：求不等式x3+4x2﹣x﹣4＞0的解集．
某同學根據學習以上知識的經驗，對求不等式x3+4x2﹣x﹣4＞0的解集進行了探究．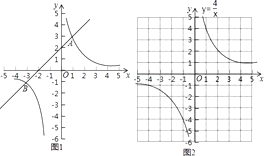
下面是他的探究過程，請將（2）、（3）、（4）補充完整：
（1）①將不等式按條件進行轉化： 當x=0時，原不等式不成立；
當x＞0時，原不等式可以轉化為x2+4x﹣1＞ 
；
當x＜0時，原不等式可以轉化為x2+4x﹣1＜ ；
②構造函數，畫出圖象
設y3=x2+4x﹣1，y4= ，在同一坐標系中分別畫出這兩個函數的圖象．
雙曲線y4= 如圖2所示，請在此坐標系中畫出拋物線y3=x2+4x﹣1；（不用列表）
（2）確定兩個函數圖象公共點的橫坐標 觀察所畫兩個函數的圖象，猜想并通過代入函數解析式驗證可知：滿足y3=y4的所有x的值為
（3）借助圖象，寫出解集 結合（1）的討論結果，觀察兩個函數的圖象可知：不等式x3+4x2﹣x﹣4＞0的解集為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
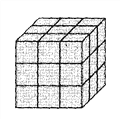
【題目】將一個正方體木塊涂成紅色，然后如圖把它的棱三等分，再沿等分線把正方體切開，可以得到27個小正方體.觀察并回答下列問題：
（1）其中三面涂色的小正方體有________個，兩面涂色的小正方體有______個，各面都沒有涂色的小正方體有________個；
（2）如果將這個正方體的棱n等分，所得的小正方體中三面涂色的有_________個，各面都沒有涂色的有________個；
（3）如果要得到各面都沒有涂色的小正方體125個, 那么應該將此正方體的棱______等分.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，O為直線AB上一點，OC平分∠AOE，∠DOE=90°，則以下結論正確的有____________．（只填序號）
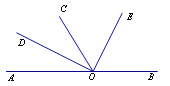
①∠AOD與∠BOE互為余角；
②OD平分∠COA；
③∠BOE=56°40′，則∠COE=61°40′；
④∠BOE=2∠COD．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面材料：
小丁在研究數學問題時遇到一個定義：對于排好順序的三個數： 
，稱為數列
.計算
， 
， 
將這三個數的最小值稱為數列
的價值．例如，對于數列2，﹣1，3，因為
， 
， 
，所以數列2，﹣1，3的價值為
．
小丁進一步發現：當改變這三個數的順序時，所得到的數列都可以按照上述方法計算其相應的價值．如數列﹣1，2，3的價值為
；數列3，﹣1，2的價值為1；…．經過研究，小丁發現，對于“2，﹣1，3”這三個數，按照不同的排列順序得到的不同數列中，價值的最小值為
．根據以上材料，回答下列問題：
（1）數列﹣4，﹣3，2的價值為 ；
（2）將“﹣4，﹣3，2”這三個數按照不同的順序排列，可得到若干個數列，這些數列的價值的最小值為 ，取得價值最小值的數列為 （寫出一個即可）；
（3）將2，﹣9，a（a＞1）這三個數按照不同的順序排列，可得到若干個數列．若這些數列的價值的最小值為1，則a的值為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
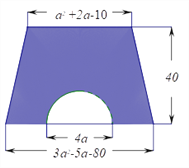
【題目】如圖，梯形的上底為
+2
-10，下底為3-5-80，高為40.（
取3）
（1）用式子表示圖中陰影部分的面積；
（2）當=10時，求陰影部分面積的值。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】同學們都知道，|5﹣（﹣2）|表示5與﹣2之差的絕對值，實際上也可理解為5與﹣2兩數在數軸上所對的兩點之間的距離．試探索：
（1）求|5﹣（﹣2）|=________．
（2）數軸上表示x和﹣1的兩點之間的距離表示為________．
（3）找出所有符合條件的整數x，使|x+5|+|x﹣2|=7，這樣的整數有________個．
查看答案和解析>>
科目：初中數學 來源： 題型：
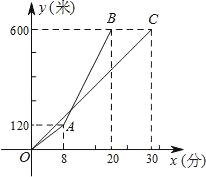
【題目】甲、乙兩人沿同一路線登山，圖中線段OC、折線OAB分別是甲、乙兩人登山的路程y（米）與登山時間x（分）之間的函數圖象．請根據圖象所提供的信息，解答如下問題：
（1）求甲登山的路程與登山時間之間的函數關系式，并寫出自變量x的取值范圍；
（2）求乙出發后多長時間追上甲？此時乙所走的路程是多少米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列三行數，并完成后面的問題：
①﹣2，4，﹣8，16，﹣32，…；
②l，﹣2，4，﹣8，16，…；
③0，﹣3，3，﹣9，15，…
（1）思考第①行數的規律，寫出第n個數字是多少（用含n的式子表示）；
（2）第②行數和第①行數有什么關系？第③行數和第②行數又有什么關系？
（3）設x，y，z分別表示第①②③行數的第10個數字，求x+y+z的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com