
【題目】某校“心靈信箱”的設立,為師、生之間的溝通開設了一個書面交流的渠道.為了解九年級學生對“心靈信箱”開通兩年來的使用情況,某課題組對該校九年級全體學生進行了一次問卷調查,并根據調查結果繪制了如下尚不完整的統計圖.
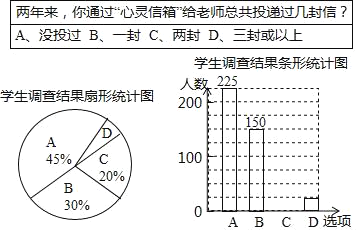
根據圖表,解答以下問題:
(1)該校九年級學生共有 人;
(2)學生調查結果扇形統計圖中,扇形D的圓心角度數是 ;
(3)請你補充條形統計圖;
(4)根據調查結果可以推斷:兩年來,該校九年級學生通過“心靈信箱”投遞出的信件總數至少有 封.
【答案】(1) 500,(2)18°(3)見解析(4)365
【解析】
(1)根據A所占的百分比和人數,可以求得該校九年級的人數;
(2)根據統計圖中的數據可以求得扇形D的圓心角度數;
(3)根據統計圖中的數據可以求得C的人數,從而可以將條形統計圖補充完整;
(4)根據統計圖中的數據可以求得投遞出的信件總數至少有多少封.
解:(1)225÷45%=500,
故答案為:500;
(2)學生調查結果扇形統計圖中,扇形D的圓心角度數是:360°×(1﹣45%﹣30%﹣20%)=18°,
故答案為:18°;
(3)C中的人數為:500×20%=100,
補充完整的條形統計圖如右圖所示;
(4)500×30%×1+500×20%×2+500×(1﹣45%﹣30%﹣20%)×3=365(封),
故答案為:365.


 名題金卷系列答案
名題金卷系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系內,拋物線![]() 與線段
與線段![]() 有兩個不同的交點,其中點
有兩個不同的交點,其中點![]() ,點
,點![]() .有下列結論:
.有下列結論:
①直線![]() 的解析式為
的解析式為![]() ;②方程
;②方程![]() 有兩個不相等的實數根;③a的取值范圍是
有兩個不相等的實數根;③a的取值范圍是![]() 或
或![]() .
.
其中,正確結論的個數為( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
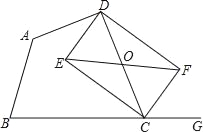
【題目】已知:如圖,在四邊形ABCD中,點G在邊BC的延長線上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于點O.
(1)求證:OE=OF;
(2)若點O為CD的中點,求證:四邊形DECF是矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解朝陽社區![]() 歲居民最喜歡的支付方式,某興趣小組對社區內該年齡段的部分居民展開了隨機問卷調查(每人只能選擇其中一項),并將調查數據整理后繪成如下兩幅不完整的統計圖.請根據圖中信息解答下列問題:
歲居民最喜歡的支付方式,某興趣小組對社區內該年齡段的部分居民展開了隨機問卷調查(每人只能選擇其中一項),并將調查數據整理后繪成如下兩幅不完整的統計圖.請根據圖中信息解答下列問題:
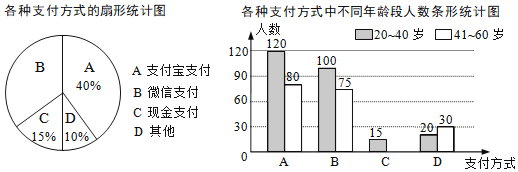
(1)求參與問卷調查的總人數.
(2)補全條形統計圖.
(3)該社區中![]() 歲的居民約8000人,估算這些人中最喜歡微信支付方式的人數.
歲的居民約8000人,估算這些人中最喜歡微信支付方式的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=8,BC=4.點G,E分別在邊AB,CD上,點F,H在對角線AC上.若四邊形EFGH是菱形,則AG的長是( )
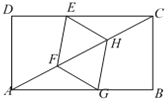
A.![]() B.5C.
B.5C.![]() D.6
D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,拋物線y=![]() x2+
x2+![]() x+3與x軸交于A、B兩點(點A在點B的右側),與y軸交于點C,過點C作x軸的平行線交拋物線于點P.連接AC.
x+3與x軸交于A、B兩點(點A在點B的右側),與y軸交于點C,過點C作x軸的平行線交拋物線于點P.連接AC.
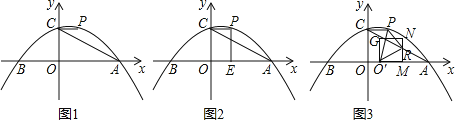
(1)求點P的坐標及直線AC的解析式;
(2)如圖2,過點P作x軸的垂線,垂足為E,將線段OE繞點O逆時針旋轉得到OF,旋轉角為α(0°<α<90°),連接FA、FC.求AF+![]() CF的最小值;
CF的最小值;
(3)如圖3,點M為線段OA上一點,以OM為邊在第一象限內作正方形OMNG,當正方形OMNG的頂點N恰好落在線段AC上時,將正方形OMNG沿x軸向右平移,記平移中的正方形OMNG為正方形O′MNG,當點M與點A重合時停止平移.設平移的距離為t,正方形O′MNG的邊MN與AC交于點R,連接O′P、O′R、PR,是否存在t的值,使△O′PR為直角三角形?若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
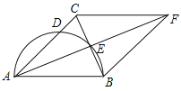
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的半圓交AC于點D,交BC于點E,延長AE至點F,使EF=AE,連接FB、FC.
(1)求證:四邊形ABFC是菱形;
(2)若AD=![]() ,BE=1,求半圓的面積.
,BE=1,求半圓的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
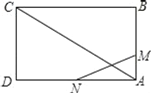
【題目】如圖,矩形ABCD的邊長AB=3cm,AC=3![]() cm,動點M從點A出發,沿AB以1cm/s的速度向點B勻速運動,同時動點N從點D出發,沿DA以2cm/s的速度向點A勻速運動.若△AMN與△ACD相似,則運動的時間t為_____s.
cm,動點M從點A出發,沿AB以1cm/s的速度向點B勻速運動,同時動點N從點D出發,沿DA以2cm/s的速度向點A勻速運動.若△AMN與△ACD相似,則運動的時間t為_____s.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com