
【題目】如圖,在△AOB中,∠AOB為直角,OA=6,OB=8,半徑為2的動圓圓心Q從點O出發,沿著OA方向以1個單位長度/秒的速度勻速運動,同時動點P從點A出發,沿著AB方向也以1個單位長度/秒的速度勻速運動,設運動時間為t秒(0<t≤5)以P為圓心,PA長為半徑的⊙P與AB、OA的另一個交點分別為C、D,連結CD、QC.
(1)當t為何值時,點Q與點D重合?
(2)當⊙Q經過點A時,求⊙P被OB截得的弦長.
(3)若⊙P與線段QC只有一個公共點,求t的取值范圍.
【答案】
(1)
解:∵OA=6,OB=8,
∴由勾股定理可求得:AB=10,
由題意知:OQ=AP=t,
∴AC=2t,
∵AC是⊙P的直徑,
∴∠CDA=90°,
∴CD∥OB,
∴△ACD∽△ABO,
∴ ![]() ,
,
∴AD= ![]() ,
,
當Q與D重合時,
AD+OQ=OA,
∴ ![]() +t=6,
+t=6,
∴t= ![]() ;
;
(2)
解:當⊙Q經過A點時,如圖1,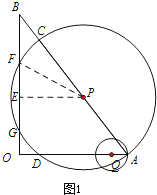
OQ=OA﹣QA=4,
∴t= ![]() =4s,
=4s,
∴PA=4,
∴BP=AB﹣PA=6,
過點P作PE⊥OB于點E,⊙P與OB相交于點F、G,
連接PF,
∴PE∥OA,
∴△PEB∽△AOB,
∴ ![]() ,
,
∴PE= ![]() ,
,
∴由勾股定理可求得:EF= ![]() ,
,
由垂徑定理可求知:FG=2EF= ![]() .
.
(3)
解:當QC與⊙P相切時,如圖2,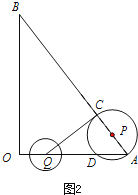
此時∠QCA=90°,
∵OQ=AP=t,
∴AQ=6﹣t,AC=2t,
∵∠A=∠A,
∠QCA=∠ABO,
∴△AQC∽△ABO,
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() ,
,
∴當0<t≤ ![]() 時,⊙P與QC只有一個交點,
時,⊙P與QC只有一個交點,
當QC⊥OA時,
此時Q與D重合,
由(1)可知:t= ![]() ,
,
∴當 ![]() <t≤5時,⊙P與QC只有一個交點,
<t≤5時,⊙P與QC只有一個交點,
綜上所述,當,⊙P與QC只有一個交點,t的取值范圍為:0<t≤ ![]() 或
或 ![]() <t≤5.
<t≤5.
【解析】(1)由題意知CD⊥OA,所以△ACD∽△ABO,利用對應邊的比求出AD的長度,若Q與D重合時,則,AD+OQ=OA,列出方程即可求出t的值; (2)由于0<t≤5,當Q經過A點時,OQ=4,此時用時為4s,過點P作PE⊥OB于點E,利用垂徑定理即可求出⊙P被OB截得的弦長;
(3)若⊙P與線段QC只有一個公共點,分以下兩種情況,①當QC與⊙P相切時,計算出此時的時間;②當Q與D重合時,計算出此時的時間;由以上兩種情況即可得出t的取值范圍.本題考查圓的綜合問題,涉及圓的切線判定,圓周角定理,相似三角形的判定與性質,學生需要根據題意畫出相應的圖形來分析,并且能綜合運用所學知識進行解答.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,四邊形 ABCD 中,AC=a,BD=b,且 AC⊥BD,順次連接四邊形ABCD各邊中點,得到四邊形A1B1C1D1,再順次連接四邊形A1B1C1D1各邊中點,得到四邊形A2B2C2D2,…,如此進行下去,得到四邊形AnBnCnDn.下列結論正確的有( )
①四邊形A2B2C2D2是矩形;
②四邊形A4B4C4D4是菱形;
③四邊形A5B5C5D5的周長是![]()
④四邊形AnBnCnDn的面積是![]()

A. ①②③ B. ②③④ C. ①② D. ②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a>0)圖象的頂點為D,其圖象與x軸的交點A、B的橫坐標分別為﹣1和3,則下列結論正確的是( ) 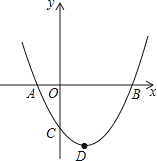
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.當a= ![]() 時,△ABD是等腰直角三角形
時,△ABD是等腰直角三角形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】同學們,我們很熟悉這樣的算式:![]() ,其實,數學不僅非常美妙,而且魅力無窮.請你欣賞下列一組等式:
,其實,數學不僅非常美妙,而且魅力無窮.請你欣賞下列一組等式:
①![]()
②![]()
③![]()
④![]()
⑤……
(1)寫出第⑤個等式:![]()
(2)根據上述規律,寫出第![]() 個等式:
個等式:
![]()
(3)觀察比較,并大膽猜想:
![]()
(4)根據(2)的規律計算![]() (寫出計算過程)
(寫出計算過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為了鼓勵居民節約用水,決定實行兩級收費制度.若每月用水量不超過14噸(含14噸),則每噸按政府補貼優惠價m元收費;若每月用水量超過14噸,則超過部分每噸按市場價n元收費.小明家3月份用水20噸,交水費49元;4月份用水18噸,交水費42元.
(1)求每噸水的政府補貼優惠價和市場價分別是多少?
(2)設每月用水量為x噸,應交水費為y元,請寫出y與x之間的函數關系式;
(3)小明家5月份用水26噸,則他家應交水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,BD為⊙O的直徑,BD與AC相交于點H,AC的延長線與過點B的直線相交于點E,且∠A=∠EBC.
(1)求證:BE是⊙O的切線;
(2)已知CG∥EB,且CG與BD、BA分別相交于點F、G,若BGBA=48,FG= ![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次男子馬拉松長跑比賽中,隨機抽得12名選手所用的時間(單位:分鐘)得到如下樣本數據:140 146 143 175 125 164 134 155 152 168 162 148
(1)計算該樣本數據的中位數和平均數;
(2)如果一名選手的成績是147分鐘,請你依據樣本數據中位數,推斷他的成績如何?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com