
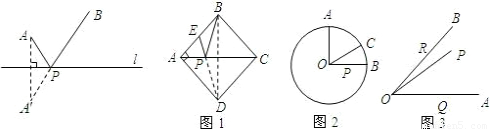
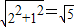 ;
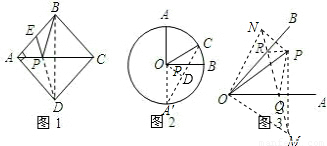
;
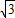
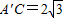 ;
;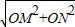 =
=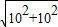 =10
=10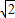 .
.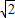 .
.

 一線名師提優試卷系列答案
一線名師提優試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源:2009年全國中考數學試題匯編《圖形的對稱》(04)(解析版) 題型:解答題
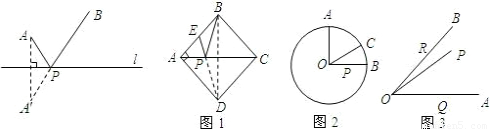
查看答案和解析>>
科目:初中數學 來源:2010年江蘇省鹽城市鹽都區中考數學一模試卷(解析版) 題型:解答題
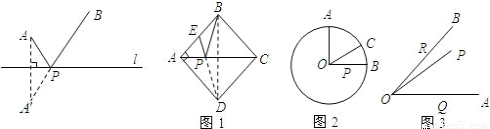
查看答案和解析>>
科目:初中數學 來源:2010年江蘇省鹽城市鞍湖實驗學校初三中考模擬試卷(解析版) 題型:解答題
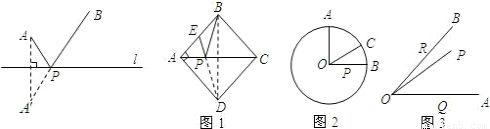
查看答案和解析>>
科目:初中數學 來源:2010年北京市延慶縣畢業考試數學試卷(解析版) 題型:解答題
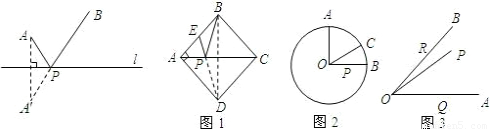
查看答案和解析>>
科目:初中數學 來源:2009年福建省漳州市中考數學試卷(解析版) 題型:解答題
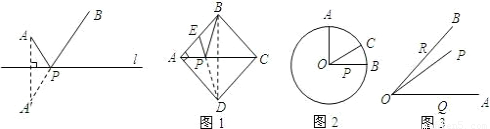
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com