
【題目】疫情期間福州一中初中部舉行了“宅家運動會”.該學校七、八年級各有300名學生參加了這次“宅家運動會”,現從七、八年級各隨機抽取20名學生宅家運動會的成績進行抽樣調查.
收集數據如下:
七年級: | 74 | 97 | 96 | 72 | 98 | 99 | 72 | 73 | 76 | 74 |
74 | 69 | 76 | 89 | 78 | 74 | 99 | 97 | 98 | 99 | |
八年級: | 76 | 88 | 96 | 89 | 78 | 94 | 89 | 94 | 95 | 50 |
89 | 68 | 65 | 89 | 77 | 86 | 89 | 88 | 92 | 91 |
整理數據如下:
|
|
|
|
| |
七年級 | 0 | 1 | 10 | 1 | a |
八年級 | 1 | 2 | 3 | 8 | 6 |
分析數據如下:
年級 | 平均數 | 中位數 | 眾數 | 方差 |
七年級 | 84.2 | 77 | 74 | 138.56 |
八年級 | 84 | b | 89 | 129.7 |
根據以上信息,回答下列問題:
(1)![]() ___________,
___________,![]() ___________;
___________;
(2)你認為哪個年級“宅家運動會”的總體成績較好,說明理由(至少從兩個不同的角度說明推斷的合理性)
(3)學校對“宅家運動會”成績不低于80分的學生頒發優勝獎,請你估計學校七、八年級所有學生中獲得優勝獎的大約有___________人.
【答案】(1) ![]() ,
,![]() ;
;
(2) 八年級成績較好,理由①:八年級成績的眾數、中位數比七年級成績相應的眾數、中位數都要大,說明八年級成績的集中趨勢要高;理由②:方差八年級較小,說明八年級的成績比較穩定;
(3) 345(人).
【解析】
(1)從調查的7年級的總人數20人中減去前幾組的人數即可;將8年級20名學生的成績排序后找到最中間的第10個和第11個數的平均是即可求出中位數;
(2)從中位數、眾數、方差等方面進行分析即可;
(3)用各個年級的總人數乘以樣本中大于等于80分所占的百分比即可.
解:(1)由題意有:![]()
將8年級的20名學生成績排序后最中間兩個數據為:89和89,故中位數為89;
故答案為:![]() ,
,![]() .
.
(2) 八年級成績較好,八年級成績的眾數、中位數比七年級成績相應的眾數、中位數都要大,說明八年級成績的集中趨勢要高,方差八年級較小,說明八年級的成績比較穩定;
(3)七年級優勝獎所占的比例為:![]() ,
,
故其300人中能獲得優勝獎的有:![]() (人),
(人),
八年級優勝獎所占的比例為:![]() ,
,
故其300人中能獲得優勝獎的有:![]() (人),
(人),
∴所有能獲得優勝獎的學生人數為:135+210=345(人).
故答案為:345(人).


科目:初中數學 來源: 題型:
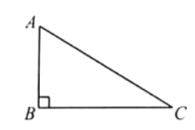
【題目】如圖,在Rt△ABC中,∠ACB=90°,過點C的直線m∥AB,D為AB邊上一點,過點D作DE⊥BC,交直線m于點E,垂足為點F,連接CD,BE.
(1)求證:CE=AD;
(2)當點D是AB中點時,四邊形BECD是什么特殊四邊形?說明你的理由;
(3)當∠A的大小滿足什么條件時,四邊形BECD是正方形?(不需要證明)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(一)知識鏈接
若點M,N在數軸上,且M,N代表的實數分別是a,b,則線段MN的長度可表示為 .
(二)解決問題
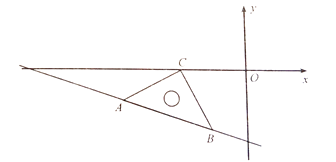
如圖,將一個三角板放置在平面直角坐標系中,∠ACB=90°,AC=BC,點B,C的坐標分別為(-2,-4),(-4,0).
(1)求點A的坐標及直線AB的表達式;
(2)若P是x軸上一點,且S△ABP=6,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小東設計的“作矩形”的尺規作圖過程,已知:![]()
求作:矩形![]()
作法:如圖,
①作線段![]() 的垂直平分線角交
的垂直平分線角交![]() 于點
于點![]() ;
;
②連接![]() 并延長,在延長線上截取
并延長,在延長線上截取![]()
③連接![]()
所以四邊形![]() 即為所求作的矩形
即為所求作的矩形
根據小東設計的尺規作圖過程
(1)使用直尺和圓規,補全圖形:(保留作圖痕跡)
(2)完成下邊的證明:
證明:![]() ,
,![]() ,
,
![]() 四邊形是平行四邊形( )(填推理的依據)
四邊形是平行四邊形( )(填推理的依據)
![]()
![]() 四邊形
四邊形![]() 是矩形( )(填推理的依據)
是矩形( )(填推理的依據)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為6的正方形ABCD內部有一點P,BP=4,∠PBC=60°,點Q為正方形邊上一動點,且△PBQ是等腰三角形,則符合條件的Q點有__________個.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場為了吸引顧客,設計了一種促銷活動.在一個不透明的箱子里放有4個完全相同的小球,球上分別標有“0元”、“10元”、“30元”、“50元”的字樣.規定:顧客在本商場同一日內,消費每滿300元,就可以從箱子里先后摸出兩個球(每次只摸出一個球,第一次摸出后不放回).商場根據兩個小球所標金額之和返還相應價格的購物券,可以重新在本商場消費.某顧客消費剛好滿300元,則在本次消費中:
(1)該顧客至少可得 元購物券,至多可得 元購物券;
(2)請用畫樹狀圖或列表法,求出該顧客所獲購物券的金額不低于50元的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
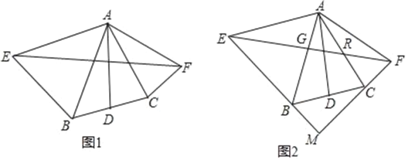
【題目】已知,如圖AD為△ABC的中線,分別以AB和AC為一邊在△ABC的外部作等腰三角形ABE和等腰三角形ACF,且AE=AB,AF=AC,連接EF,∠EAF+∠BAC=180°
(1)如圖1,若∠ABE=63°,∠BAC=45°,求∠FAC的度數;
(2)如圖1請探究線段EF和線段AD有何數量關系?并證明你的結論;
(3)如圖2,設EF交AB于點G,交AC于點R,延長FC,EB交于點M,若點G為線段EF的中點,且∠BAE=70°,請探究∠ACB和∠CAF的數量關系,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() 與⊙O相離,OA⊥
與⊙O相離,OA⊥![]() 于點A,交⊙O于點P,點B是⊙O上一點,連接BP并延長,交直線
于點A,交⊙O于點P,點B是⊙O上一點,連接BP并延長,交直線![]() 于點C,使得AB=AC.
于點C,使得AB=AC.

(1)求證:AB是⊙O的切線;
(2)若PC=2![]() ,OA=4,求⊙O的半徑.
,OA=4,求⊙O的半徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com