
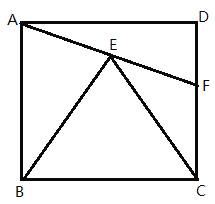
【題目】如圖,在正方形![]() 內作正三角形
內作正三角形![]() ,連接
,連接![]() 并延長
并延長![]() 交于F,則
交于F,則![]() 為_______________
為_______________![]() ,若
,若![]() ,則
,則![]() 長度為__________.
長度為__________.
【答案】![]()
![]()
【解析】
由正方形![]() 內作正三角形
內作正三角形![]() ,得∠BAE=∠BEA=75°,從而得∠DAF=15°,即可求出
,得∠BAE=∠BEA=75°,從而得∠DAF=15°,即可求出![]() ,在AD邊上取點M,使AM=FM,由含30°角的直角三角形的性質,得AM=MF=
,在AD邊上取點M,使AM=FM,由含30°角的直角三角形的性質,得AM=MF=![]() ,MD=
,MD=![]() ,進而即可求解.
,進而即可求解.
∵在正方形![]() 內作正三角形
內作正三角形![]() ,
,
∴BE=BC=AB,∠EBC=60°,
∴∠ABE=90°-60°=30°,
∴∠BAE=∠BEA=(180°-30°)÷2=75°,
∴∠DAF=90°-75°=15°,
∴![]() =90°+15°=105°;
=90°+15°=105°;
在AD邊上取點M,使AM=FM,則∠MFA=∠MAF=15°,
∴∠DMF=15°+15°=30°,
∵![]() ,
,
∴AM=MF=![]() =
=![]() ,MD=
,MD=![]() ,
,
∴AD=AM+MD=![]() +
+![]() =
=![]() ,
,
∴CD=AD=![]() ,
,
∴![]() =CD-DF=(
=CD-DF=(![]() )-(
)-(![]() )=2.
)=2.
故答案是:105;2.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】若二次函數y=ax2+bx+c(a≠0)中,函數值y與自變量x的部分對應值如表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -2 | -2 | 0 | 4 | … |
(1)求該二次函數的表達式;
(2)當y≥4時,求自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
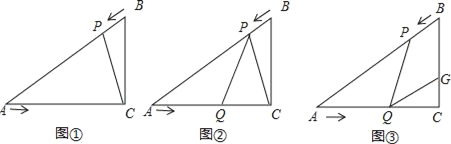
【題目】已知:如圖,在Rt△ACB中,∠C=90°,BC=3cm,AC=3![]() cm,點P由B點出發沿BA方向向點A勻速運動,速度為2cm/s;點Q由A點出發沿AC方向向點C勻速運動,速度為
cm,點P由B點出發沿BA方向向點A勻速運動,速度為2cm/s;點Q由A點出發沿AC方向向點C勻速運動,速度為![]() cm/s;若設運動的時間為t(s)(0<t<3),解答下列問題:
cm/s;若設運動的時間為t(s)(0<t<3),解答下列問題:
(1)如圖①,連接PC,當t為何值時△APC∽△ACB,并說明理由;
(2)如圖②,當點P,Q運動時,是否存在某一時刻t,使得點P在線段QC的垂直平分線上,請說明理由;
(3)如圖③,當點P,Q運動時,線段BC上是否存在一點G,使得四邊形PQGB為菱形?若存在,試求出BG長;若不存在請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
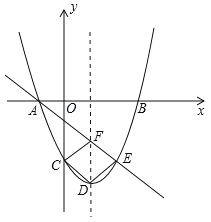
【題目】如圖,二次函數y=x2+bx+c的圖象與x軸相交于點A、B兩點,與y軸相交于點C(0,﹣3),拋物線的對稱軸為直線x=1.
(1)求此二次函數的解析式;
(2)若拋物線的頂點為D,點E在拋物線上,且與點C關于拋物線的對稱軸對稱,直線AE交對稱軸于點F,試判斷四邊形CDEF的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 、點
、點![]() 分別在線段
分別在線段![]() 、線段
、線段![]() 上運動(不包含端點),以
上運動(不包含端點),以![]() 為邊作平行四邊形
為邊作平行四邊形![]() ,點
,點![]() 從
從![]() 向
向![]() 運動,速度為每秒
運動,速度為每秒![]() 個單位長度,點
個單位長度,點![]() 從
從![]() 向
向![]() 運動,速度為每秒
運動,速度為每秒![]() 個單位長度,兩點同時出發,當一個點到達終點時,兩點都停止運動,運動時間為
個單位長度,兩點同時出發,當一個點到達終點時,兩點都停止運動,運動時間為![]() 秒.
秒.
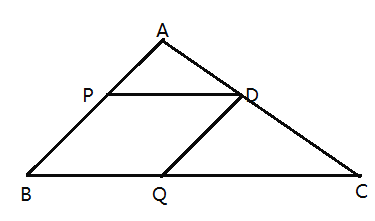
(1)![]() __ ,
__ ,![]() __ _; (用
__ _; (用![]() 表示)
表示)
(2)當平行四邊形![]() 為菱形時,求出
為菱形時,求出![]() 值;
值;
(3)![]() 點能否落在線段
點能否落在線段![]() 上?若能,求出
上?若能,求出![]()
(4)當![]() 分別與線段
分別與線段![]() 交于
交于![]() 兩點時,求
兩點時,求![]() 長度的范圍;
長度的范圍;
(5)平行四邊形![]() 的面積能否為
的面積能否為![]() 面積的一半,若能,請求出
面積的一半,若能,請求出![]() 值,若不能,請說明理由.
值,若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店將每件進價為80元的某種商店按每件110元出售,每天可售出100件.該商店想通過降低售價、增加銷售量的方法來提高利潤.經市場調查,發現這種商品每件每降價5元,每天的銷售量可增加50件.設商品降價x元,每天銷售該商品獲得的利潤為y元.
(1)求y(元)關于x(元)的函數關系式,并寫出x的取值范圍.
(2)求當x取何值時y最大?并求出y的最大值.
(3)若要是每天銷售利潤為3750元,且盡可能最大的向顧客讓利,應將該商品降價多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com