
【題目】在平面直角坐標系中,已知兩點A(-4,0)、B(1,0),且以AB為直徑的圓交![]() 軸的正半軸于點C(0,2),過點C作圓的切線交x軸于點D.
軸的正半軸于點C(0,2),過點C作圓的切線交x軸于點D.

(1)求過A, B,C三點的拋物線解析式;
(2)求點D的坐標;
(3)設平行于x軸的直線交拋物線于E,F兩點,問是否存在以線段EF為直徑的圓,恰好與x軸相切?若存在,求出該圓的半徑,若不存在,請說明理由.
【答案】(1)![]() ;(2)D的坐標為(
;(2)D的坐標為(![]() ,0);(3)存在,
,0);(3)存在, ![]() 或
或![]() .
.
【解析】(1)已知了拋物線過A,B,C三點,可根據三點的坐標用待定系數法求出拋物線的解析式.
(2)由于CD是圓的切線,設圓心為O′,可連接O′C,在直角三角形O′CD中科根據射影定理求出OD的長,即可得出D的坐標.
(3)可假設存在這樣的點E、F,設以線段EF為直徑的圓的半徑為|r|,那么可用半徑|r|表示出E,F兩點的坐標,然后根據E,F在拋物線上,將E,F的坐標代入拋物線的解析式中,可得出關于|r|的方程,如果方程無解則說明不存在這樣的E,F點,如果方程有解,可用得出的r的值求出E,F兩點的坐標.
解:(1)設二次函數的解析式為![]() ,則
,則
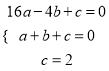 ,
,  ,
,
故拋物線的解析式為![]() .
.
過圓心O′做拋物線的對稱軸,連接O′C.
(2)如圖所示,
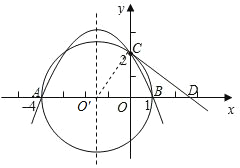
以![]() 為直徑的圓圓心坐標為O′(
為直徑的圓圓心坐標為O′(![]() ,0).
,0).
![]() ,
, ![]() .
.
∵CD為⊙O′切線
∴O′C⊥CD,
∵ ∠O′OC=∠COD=90°
∴ ∠CDO+∠DCO=∠CDO+∠CO′O=90°
∴ ∠DCO=∠CO′O
∴ ⊿O′CO∽⊿CDO, ![]() ,
,
∴ ,
,
![]() .
.
∴ D的坐標為(![]() ,0).
,0).
(3)存在.拋物線對稱軸為![]() .設圓的半徑為r(r>0),令點
.設圓的半徑為r(r>0),令點![]() 在點F的左邊.
在點F的左邊.
①當E,F在![]() 軸上方時,則E坐標為(
軸上方時,則E坐標為(![]() -r,r),F坐標為(
-r,r),F坐標為(![]() +r,r)將點E坐標代入拋物線
+r,r)將點E坐標代入拋物線
![]() 中,得r=
中,得r=![]() (
(![]() -r)2-
-r)2-![]() (-
(-![]() -r)+2,
-r)+2,
![]() ,
, ![]() (舍去).
(舍去).
②當E,F在x軸下方時,則E坐標為(-![]() -r,-r),F坐標為(-
-r,-r),F坐標為(-![]() +r,-r),將E點的坐標代入
+r,-r),將E點的坐標代入![]() .得-r=-(-
.得-r=-(-![]() -r)2-
-r)2-![]() (-
(-![]() -r)+2,得r3=1+
-r)+2,得r3=1+![]() 或r4=1-
或r4=1-![]() (舍去) .
(舍去) .
故在以![]() 為直徑的圓,恰好與
為直徑的圓,恰好與![]() 軸相切,該圓的半徑為
軸相切,該圓的半徑為![]() 或
或![]() .
.
“點睛”本題著重考查了待定系數法求二次函數解析式、三角形相似、切線的性質等重要知識點,綜合性強,考查學生數形結合的數學思想方法.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=10厘米,BC=8厘米,點D為AB的中點,如果點P在線段BC上以3厘米/秒的速度由B點向C點運動,同時點Q在線段CA上由C點向A點運動,當一個點停止運動時,另一個點也隨之停止運動,當點Q的運動速度為時,能夠在某一時刻使△BPD與△CQP全等. 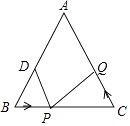
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B兩地的距離是80千米,一輛公共汽車從A地駛出3小時后,一輛小汽車也從A地出發,它的速度是公共汽車的3倍,已知小汽車比公共汽車遲20分鐘到達B地,求兩車的速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】角平分線上的點到角兩邊的距離相等.這一性質在解決圖形面積問題時有何妙用呢?閱讀材料:已知,如圖(1),在面積為S的△ABC中,BC=a,AC=b,AB=c,三條角平分線的交點O到三邊的距離為r.連接OA、OB、OC,△ABC被劃分為三個小三角形.
∵S=S△OBC+S△OAC+S△OAB= ![]() BCr+
BCr+ ![]() ACr+
ACr+ ![]() ABr=
ABr= ![]() (a+b+c)r,∴r=
(a+b+c)r,∴r= ![]()

(1)類比推理:若面積為S的四邊形ABCD的四條角平分線交于O點,如圖(2),各邊長分別為AB=a,BC=b,CD=c,AD=d,求點O到四邊的距離r;
(2)理解應用:如圖(3),在四邊形ABCD中,AB∥DC,AB=21,CD=11,AD=BC=13,對角線BD=20,點O1與O2分別為△ABD與△BCD的三條角平分線的交點,設它們到各自三角形三邊的距離為r1和r2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若二次函數y=ax2+bx+c的圖象經過點(﹣1,0)和(3,0),則方程ax2+bx+c=0的解為( )
A.x1=﹣3,x2=﹣1B.x1=1,x2=3
C.x1=﹣1,x2=3D.x1=﹣3,x2=1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列條件中不可以判定兩個直角三角形全等的是( )
A. 兩條直角邊對應相等 B. 斜邊和直角邊對應相等
C. 一條邊和一銳角對應相等 D. 兩個角對應相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB邊的垂直平分線l1交BC于D,AC邊的垂直平分線l2交BC于E,l1與l2相交于點O.△ADE的周長為6cm. 
(1)求BC的長;
(2)分別連結OA、OB、OC,若△OBC的周長為16cm,求OA的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com