
 如圖,直線AB的解析式為y=
如圖,直線AB的解析式為y=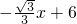 ,分別與x軸、y軸相交于B、A兩點.點C在射線BA上以3cm/秒的速度運動,以C點為圓心作半徑為1cm的⊙C.點P以2cm/秒的速度在線段OA上來回運動,過點P作直線l垂直與y軸.若點C與點P同時從點B、點O開始運動,設運動時間為t秒,則在整個運動過程中直線l與⊙C共有________次相切;直線l與⊙C最后一次相切時t=________.
,分別與x軸、y軸相交于B、A兩點.點C在射線BA上以3cm/秒的速度運動,以C點為圓心作半徑為1cm的⊙C.點P以2cm/秒的速度在線段OA上來回運動,過點P作直線l垂直與y軸.若點C與點P同時從點B、點O開始運動,設運動時間為t秒,則在整個運動過程中直線l與⊙C共有________次相切;直線l與⊙C最后一次相切時t=________.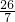
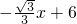 ,分別與x軸、y軸相交于B、A兩點.即可求得點A與B的坐標,則可求得∠ABO的度數,得到BC=2CD;然后分別從直線l與⊙C第一次相切,第二次相切,第三次相切,去分析求解,即可求得答案.
,分別與x軸、y軸相交于B、A兩點.即可求得點A與B的坐標,則可求得∠ABO的度數,得到BC=2CD;然后分別從直線l與⊙C第一次相切,第二次相切,第三次相切,去分析求解,即可求得答案. 解:過點C作CD⊥x軸于點D,
解:過點C作CD⊥x軸于點D,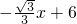 ,分別與x軸、y軸相交于B、A兩點,
,分別與x軸、y軸相交于B、A兩點, ,
, ,0),
,0), ,
,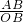 =
= ,
, ∴3t=2(12-2t-1),
∴3t=2(12-2t-1),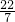 ;
;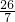 .
.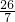 .
.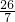 .
.

 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
 14、如圖,直線AB的解析式為y1=k1x-2k1,直線AC的解析式為y2=k2x+b,它們分別與x軸交于點B、C,且A點的橫坐標為1,則B點的坐標為
14、如圖,直線AB的解析式為y1=k1x-2k1,直線AC的解析式為y2=k2x+b,它們分別與x軸交于點B、C,且A點的橫坐標為1,則B點的坐標為查看答案和解析>>
科目:初中數學 來源: 題型:
 |
| GF |
 |
| GF |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,直線AB的解析式為y=-
如圖,直線AB的解析式為y=-
| ||
| 3 |
| 26 |
| 7 |
| 26 |
| 7 |
查看答案和解析>>
科目:初中數學 來源:2011-2012學年江蘇省無錫市輔仁中學九年級(下)期中數學試卷(解析版) 題型:填空題
 ,分別與x軸、y軸相交于B、A兩點.點C在射線BA上以3cm/秒的速度運動,以C點為圓心作半徑為1cm的⊙C.點P以2cm/秒的速度在線段OA上來回運動,過點P作直線l垂直與y軸.若點C與點P同時從點B、點O開始運動,設運動時間為t秒,則在整個運動過程中直線l與⊙C共有 次相切;直線l與⊙C最后一次相切時t= .
,分別與x軸、y軸相交于B、A兩點.點C在射線BA上以3cm/秒的速度運動,以C點為圓心作半徑為1cm的⊙C.點P以2cm/秒的速度在線段OA上來回運動,過點P作直線l垂直與y軸.若點C與點P同時從點B、點O開始運動,設運動時間為t秒,則在整個運動過程中直線l與⊙C共有 次相切;直線l與⊙C最后一次相切時t= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com