
 如圖,直線L1經過原點,與雙曲線y=
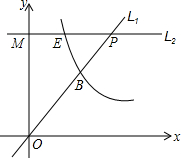
如圖,直線L1經過原點,與雙曲線y= (x>0)交于點B(1,2),點M為y正半軸上一點,過M作直線L2∥x軸交L1于P,交雙曲線y=
(x>0)交于點B(1,2),點M為y正半軸上一點,過M作直線L2∥x軸交L1于P,交雙曲線y= (x>0)于E.
(x>0)于E. (x>0)的解析式;
(x>0)的解析式; (x>0)于F,判斷點F是否為PN中點?若是求點F坐標,若不是,求PF與NF的比值.
(x>0)于F,判斷點F是否為PN中點?若是求點F坐標,若不是,求PF與NF的比值.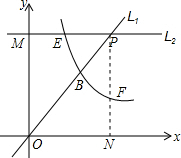 解:(1)設直線L1的解析式為y=mx,
解:(1)設直線L1的解析式為y=mx, 得k=1×2=2,
得k=1×2=2, ;
; a,2a),
a,2a), a,2a)代入y=
a,2a)代入y= 得
得 a•2a=2,解得a=
a•2a=2,解得a= 或a=-
或a=- (舍去),
(舍去), ,0);
,0); ,2
,2 ),
), ,F點的橫坐標為
,F點的橫坐標為 ,
, 代入y=
代入y= 得y=
得y= =
= ,
, ,
, ),
), ,
, 求出k,從而確定反比例函數解析式為y=
求出k,從而確定反比例函數解析式為y= ;
; a,2a),再把E(
a,2a),再把E( a,2a)代入反比例函數解析式求出滿足條件的a的值,于是可得到M點坐標為(
a,2a)代入反比例函數解析式求出滿足條件的a的值,于是可得到M點坐標為( ,0);
,0); ,2
,2 ),再利用PN⊥x軸,得到PN=2
),再利用PN⊥x軸,得到PN=2 ,且F點的橫坐標為
,且F點的橫坐標為 ,然后把x=
,然后把x= 代入反比例函數解析式求出對應的函數值,則可確定F點的坐標為(
代入反比例函數解析式求出對應的函數值,則可確定F點的坐標為( ,
, ),所以FN=
),所以FN= ,則PN=2FN,于是可判斷F點為PN的中點.
,則PN=2FN,于是可判斷F點為PN的中點.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
| 15 |
| 4 |
 的平行線,與CD交于點Q,以PQ為邊向右作正方形PQEF.設點P的橫坐標為t.
的平行線,與CD交于點Q,以PQ為邊向右作正方形PQEF.設點P的橫坐標為t.| 9 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 |
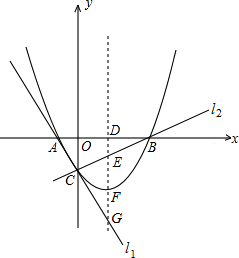 ,拋物線y=ax2+bx+c(a≠0)經過A、B、C三點.
,拋物線y=ax2+bx+c(a≠0)經過A、B、C三點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
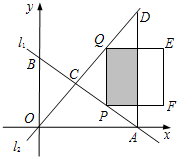
 ),且OA=8.在直線AB上取點P,過點P作y軸
),且OA=8.在直線AB上取點P,過點P作y軸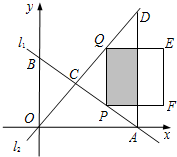 的平行線,與CD交于點Q,以PQ為邊向右作正方形PQEF.設點P的橫坐標為t.
的平行線,與CD交于點Q,以PQ為邊向右作正方形PQEF.設點P的橫坐標為t. ,在點P的運動過程中,點M能否在正方形PQEF內部?若能,求出t的取值范圍;若不能,試說明理由.
,在點P的運動過程中,點M能否在正方形PQEF內部?若能,求出t的取值范圍;若不能,試說明理由.查看答案和解析>>
科目:初中數學 來源:2012年貴州省畢節地區中考數學試卷(解析版) 題型:解答題
 ),拋物線y=ax2+bx+c(a≠0)經過A、B、C三點.
),拋物線y=ax2+bx+c(a≠0)經過A、B、C三點.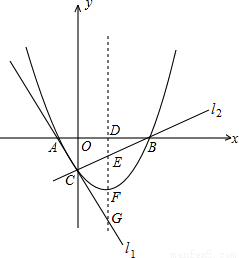
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com