
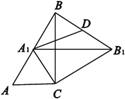
【題目】如圖,RtΔABC中∠C=90°,∠ABC=30°,ΔABC繞點C順時針旋轉得ΔA1B1C,當A1落在AB上時,連接B1B,取B1B的中點D,連接A1D,則![]() 的值為_______.
的值為_______.
【答案】![]()
【解析】
根據旋轉的性質得到△ACA1和△BCB1是等邊三角形,再根據等邊三角形的內角度數及直角三角形的內角度數推出△A1BD為直角三角形,設AC=x,根據勾股定理得出A1B=x,BB1=![]() x,因為點D是BB1的中點,得出BD =
x,因為點D是BB1的中點,得出BD =![]() x,根據勾股定理得出A1D=
x,根據勾股定理得出A1D=![]() =
=![]() ,從而可得出
,從而可得出![]() 的值.
的值.
解:∵∠ACB=90°,∠ABC=30°
∴∠A=90°-∠ABC=90°-30°=60°
∵△ABC繞點C順時針旋轉得△A1B1C
∴CA=CA1,CB=CB1
∴△ACA1是等邊三角形
∴∠ACA1=60°
∴∠A1CB=∠ACB-∠ACA1=90°-60°=30°
∵∠A1CB1=90°
∴∠BCB1=∠A1CB1-∠A1CB=90°-30°=60°
∵CB=CB1
∴△BCB1是等邊三角形
∴∠B1BC=60°
∴∠A1BB1=∠ABC+∠B1BC=30°+60°=90°
設AC=x,
則在Rt△ABC中,A1C=AA1=AC=x,AB=2x,BC=![]() x
x
∴A1B=x,BB1=![]() x
x
∵點D是BB1的中點
∴BD=![]() BB1=
BB1=![]() x
x
在Rt△A1BD中,
A1D=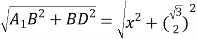 =
=![]()
∴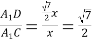
故答案為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】將一大、一小兩個等腰直角三角形拼在一起,![]() ,連接
,連接![]() .
.
(1)如圖1,若![]() 三點在同一條直線上,則
三點在同一條直線上,則![]() 與
與![]() 的關系是 ;
的關系是 ;
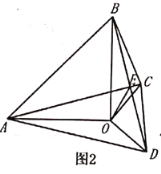
(2)如圖2,若![]() 三點不在同一條直線上,
三點不在同一條直線上,![]() 與
與![]() 相交于點
相交于點![]() ,連接
,連接![]() ,猜想
,猜想![]() 之間的數量關系,并給予證明;
之間的數量關系,并給予證明;
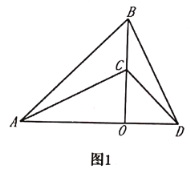
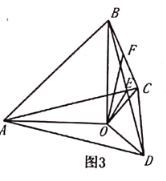
(3)如圖3,在(2)的條件下作![]() 的中點
的中點![]() ,連接
,連接![]() ,直接寫出
,直接寫出![]() 與
與![]() 之間的關系.
之間的關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(題文)“校園詩歌大賽”結束后,張老師和李老師將所有參賽選手的比賽成績(得分均為整數)進行整理,并分別繪制成扇形統計圖和頻數直方圖部分信息如下:
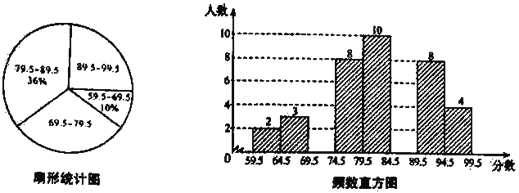
(1)本次比賽參賽選手共有 人,扇形統計圖中“69.5~79.5”這一組人數占總參賽人數的百分比為 ;
(2)賽前規定,成績由高到低前60%的參賽選手獲獎.某參賽選手的比賽成績為78分,試判斷他能否獲獎,并說明理由;
(3)成績前四名是2名男生和2名女生,若從他們中任選2人作為獲獎代表發言,試求恰好選中1男1女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
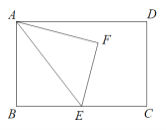
【題目】如圖,在矩形ABCD中,AB=10,BC=m,E為BC邊上一點,沿AE翻折△ABE,點B落在點F處.
(1)連接CF,若CF//AE,求EC的長(用含m的代數式表示);
(2)若EC=![]() ,當點F落在矩形ABCD的邊上時,求m的值;
,當點F落在矩形ABCD的邊上時,求m的值;
(3)連接DF,在BC邊上是否存在兩個不同位置的點E,使得?若存![]() 在,直接寫出m的取值范圍;若不存在,說明理由.
在,直接寫出m的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某養殖場計劃今年養殖無公害標準化龍蝦和鯉魚,由于受養殖水面的制約,這兩個品種的苗種的總投放量只有50噸.根據經驗測算,這兩個品種的種苗每投放一噸的先期投資、養殖期間的投資以及產值如下表:(單位:千元/噸)
品種 | 先期投資 | 養殖期間投資 | 產值 |
鯉魚 | 9 | 3 | 30 |
龍蝦 | 4 | 10 | 20 |
養殖場受經濟條件的影響,先期投資不超過360千元,養殖期間的投資不超過290千元.設鯉魚種苗的投放量為x噸.
(1)求x的取值范圍;
(2)設這兩個品種產出后的總產值為y(千元),試寫出y與x之間的函數關系式,并求出當x等于多少時,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市教育行政部門為了解初中學生參加綜合實踐活動的情況,隨機抽取了本市初一、初二、初三年級各![]() 名學生進行了調查,調查結果如圖所示,請你根據圖中的信息回答問題.
名學生進行了調查,調查結果如圖所示,請你根據圖中的信息回答問題.

(1)在被調查的學生中,參加綜合實踐活動的有多少人,參加科技活動的有多少人;
(2)如果本市有![]() 萬名初中學生,請你估計參加科技活動的學生約有多少名.
萬名初中學生,請你估計參加科技活動的學生約有多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年3月“停課不停學”期間,某校采用簡單隨機抽樣的方式調查本校學生參加第一天線上學習的時長,將收集到的數據制成不完整的頻數分布表和扇形圖,如下所示:
組別 | 學習時長(分鐘) | 頻數(人) |
第1組 | x≤40 | 3 |
第2組 | 40<x≤60 | 6 |
第3組 | 60<x≤80 | m |
第4組 | 80<x≤100 | 18 |
第5組 | 100<x≤120 | 14 |

(1)求m,n的值;
(2)學校有學生2400人,學校決定安排老師給““線上學習時長”在x≤60分鐘范圍內的學生打電話了解情況,請你根據樣本估計學校學生“線上學習時長”在x≤60分鐘范圍內的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 與x軸的交點為A,B,與y軸交于C.
與x軸的交點為A,B,與y軸交于C.
(1)求拋物線的對稱軸和點C坐標;
(2)橫、縱坐標都是整數的點叫做整點.拋物線在點A,B之間的部分與線段![]() 所圍成的區域為圖形W(不含邊界).
所圍成的區域為圖形W(不含邊界).
①當![]() 時,求圖形W內的整點個數;
時,求圖形W內的整點個數;
②若圖形W內有2個整數點,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
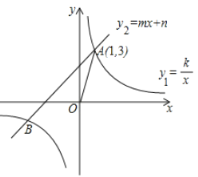
【題目】如圖,反比例函數![]() 和一次函數
和一次函數![]() 相交于點
相交于點![]() ,
,![]() .
.
(1)求一次函數和反比例函數解析式;
(2)連接OA,試問在x軸上是否存在點P,使得![]() 為以OA為腰的等腰三角形,若存在,直接寫出滿足題意的點P的坐標;若不存在,說明理由.
為以OA為腰的等腰三角形,若存在,直接寫出滿足題意的點P的坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com