
【題目】若二次函數![]() 的圖象的頂點在
的圖象的頂點在![]() 的圖象上,則稱
的圖象上,則稱![]() 為
為![]() 的伴隨函數,如
的伴隨函數,如![]() 是
是![]() 的伴隨函數.
的伴隨函數.
(1)若函數![]() 是
是![]() 的伴隨函數,求
的伴隨函數,求![]() 的值;
的值;
(2)已知函數![]() 是
是![]() 的伴隨函數.
的伴隨函數.
①當點(2,-2)在二次函數![]() 的圖象上時,求二次函數的解析式;
的圖象上時,求二次函數的解析式;
②已知矩形![]() ,
,![]() 為原點,點
為原點,點![]() 在
在![]() 軸正半軸上,點
軸正半軸上,點![]() 在
在![]() 軸正半軸上,點
軸正半軸上,點![]() (6,2),當二次函數
(6,2),當二次函數![]() 的圖象與矩形
的圖象與矩形![]() 有三個交點時,求此二次函數的頂點坐標.
有三個交點時,求此二次函數的頂點坐標.
【答案】(1)![]() ;(2)①
;(2)①![]() 或
或![]() ;②頂點坐標是(1,3)或(4,6).
;②頂點坐標是(1,3)或(4,6).
【解析】
(1)將函數![]() 的圖象的頂點坐標是(1,1),代入
的圖象的頂點坐標是(1,1),代入![]() 即可求出t的值;
即可求出t的值;
(2)①設二次函數為![]() ,根據伴隨函數定義,得出
,根據伴隨函數定義,得出![]() 代入二次函數得到:
代入二次函數得到:![]() ,把(2,-2),即可得出答案;
,把(2,-2),即可得出答案;
②由①可知二次函數為![]() ,把(0,2)代入
,把(0,2)代入![]() ,得出h的值,進行取舍即可,把(6,2)代入
,得出h的值,進行取舍即可,把(6,2)代入![]() 得出h的值,進行取舍即可.
得出h的值,進行取舍即可.
解:(1)函數![]() 的圖象的頂點坐標是(1,1),
的圖象的頂點坐標是(1,1),
把![]() ,
,![]() 代入
代入![]() ,得
,得![]() ,解得:
,解得:![]() .
.
(2)①設二次函數為![]() .
.
![]() 二次函數
二次函數![]() 是
是![]() 的伴隨函數,
的伴隨函數,![]() ,
,
![]() 二次函數為
二次函數為![]() ,
,
把![]() ,
,![]() 代入
代入![]() 得
得![]() ,
,
![]()
![]() ,
,![]() 二次函數的解析式是
二次函數的解析式是![]() 或
或![]() .
.
②由①可知二次函數為![]() ,
,
把(0,2)代入![]() ,得
,得![]() ,
,
解得![]() ,
,
當![]() 時,二次函數的解析式是
時,二次函數的解析式是![]() ,頂點是(0,2)
,頂點是(0,2)
由于此時![]() 與矩形
與矩形![]() 有三個交點時只有兩個交點
有三個交點時只有兩個交點
∴![]() 不符合題意,舍去
不符合題意,舍去
∴當![]() 時,二次函數的解析式是
時,二次函數的解析式是![]() ,頂點坐標為(1,3).
,頂點坐標為(1,3).
把(6,2)代入![]() 得
得![]() ,
,
解得![]() ,
,![]() ,
,
當![]() 時,二次函數的解析式是
時,二次函數的解析式是![]() ,頂點是(9,11)
,頂點是(9,11)
由于此時![]() 與矩形
與矩形![]() 有三個交點時只有兩個交點
有三個交點時只有兩個交點
∴![]() 不符合題意,舍去
不符合題意,舍去
∴當![]() 時,二次函數的解析式是
時,二次函數的解析式是![]() ,頂點坐標為(4,6).
,頂點坐標為(4,6).
綜上所述:頂點坐標是(1,3)或(4,6).


科目:初中數學 來源: 題型:
【題目】已知正方形MNOK和正六邊形ABCDEF邊長均為1,把正方形放在正六邊形中,使OK邊與AB邊重合,如圖所示:按下列步驟操作:將正方形在正六邊形中繞點B順時針旋轉,使KM邊與BC邊重合,完成第一次旋轉;再繞點C順時針旋轉,使MN邊與CD邊重合,完成第二次旋轉……連續經過六次旋轉.在旋轉的過程中,當正方形和正六邊形的邊重合時,點B,M間的距離可能是( )
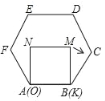
A. 0.5B. 0.7C. ![]() ﹣1D.
﹣1D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),在Rt△ABC中,∠BAC=90°,AD⊥BC于點D,點O是AC邊上的一點,連接BO交AD于點F,OE⊥OB交BC邊于點E.
(1)試說明:△ABF∽△COE.
(2)如圖(2),當O為AC邊的中點,且![]() 時,求
時,求![]() 的值.
的值.
(3)當O為AC邊的中點,![]() 時,請直接寫出
時,請直接寫出![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在利用圖象法求方程x2=![]() x+3的解x1,x2時,下面是四位同學的解法:
x+3的解x1,x2時,下面是四位同學的解法:
甲:函數y=x2﹣![]() x﹣3的圖象與x軸交點的橫坐標是x1,x2
x﹣3的圖象與x軸交點的橫坐標是x1,x2
乙:函數y=x2與y=![]() x+3的圖象交點的橫坐標是x1,x2
x+3的圖象交點的橫坐標是x1,x2
丙:函數y=x2﹣3與y=![]() x的圖象交點的橫坐標是x1,x2
x的圖象交點的橫坐標是x1,x2
丁:函數y=x2+1與y=![]() x+4的圖象交點的橫坐標是x1,x2
x+4的圖象交點的橫坐標是x1,x2
你認為解法正確的同學有_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
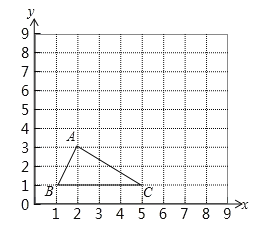
【題目】如圖,在平面直角坐標系中,![]() 三個頂點的坐標分別為A(2,3)、B(1,1)、C(5,1).
三個頂點的坐標分別為A(2,3)、B(1,1)、C(5,1).
(1)把![]() 平移后,其中點
平移后,其中點![]() 移到點
移到點![]() ,面出平移后得到的
,面出平移后得到的![]() ;
;
(2)把![]() 繞點
繞點![]() 按逆時針方向旋轉
按逆時針方向旋轉![]() ,畫出旋轉后得到的
,畫出旋轉后得到的![]() ,并求出旋轉過程中點
,并求出旋轉過程中點![]() 經過的路徑長(結果保留根號和
經過的路徑長(結果保留根號和![]() ).
).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx﹣3的圖象與x軸交于A、B與y軸交于點C,頂點坐標為(1,﹣4)
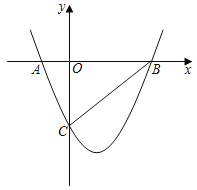
(1)求二次函數解析式;
(2)該二次函數圖象上是否存在點M,使S△MAB=S△CAB,若存在,求出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分7分)
四張質地相同的卡片如圖所示.將卡片洗勻后,背面朝上放置在桌面上.
(1)求隨機抽取一張卡片,恰好得到數字2的概率;
(2)小貝和小晶想用以上四張卡片做游戲,游戲規則見信息圖.你認為這個游戲公平嗎?請用列表法或畫樹狀圖法說明理由,若認為不公平,請你修改規則,使游戲變得公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形網格中,△ABC的頂點均在格點上,點A、B的坐標分別是A(4,3)、B(4,1),把△ABC繞點C逆時針旋轉90°后得到△A1B1C.

(1)畫出△A1B1C,直接寫出點A1、B1的坐標;
(2)求在旋轉過程中,△ABC所掃過的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
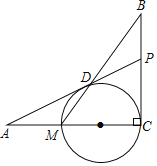
【題目】如圖,已知BC⊥AC,圓心O在AC上,點M與點C分別是AC與⊙O的交點,點D是MB與⊙O的交點,點P是AD延長線與BC的交點,且![]() .
.
(1)求證:PD是⊙O的切線;
(2)若AD=12,AM=MC,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com