
【題目】在平面直角坐標系中,直線![]() :
:![]() 與直線
與直線![]() :
:![]() 且相交于點
且相交于點![]() ,直線
,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,直線
,直線![]() 與直線
與直線![]() ,
,![]() 分別相交于點
分別相交于點![]() 、
、![]() ,點
,點![]() 是線段
是線段![]() 的中點,以點
的中點,以點![]() 為頂點的拋物線
為頂點的拋物線![]() 經過點
經過點![]() .
.
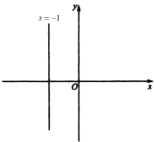
(1)①點![]() 的坐標是________;
的坐標是________;
②點![]() 的坐標是________.(用含
的坐標是________.(用含![]() 、
、![]() 的代數式表示)
的代數式表示)
(2)求![]() 的值(用含
的值(用含![]() 、
、![]() 的代數式表示);
的代數式表示);
(3)若![]() ,當
,當![]() 時,
時,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)①![]() ,②
,②![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的取值范圍是
的取值范圍是![]() 或
或![]() .
.
【解析】
(1)①由![]() 與x軸交于點B求得;
與x軸交于點B求得;
②根據直線![]() 與直線
與直線![]() ,
,![]() 分別相交于點
分別相交于點![]() 、
、![]() ,分別求出點C、D的坐標,利用點
,分別求出點C、D的坐標,利用點![]() 是線段
是線段![]() 的中點利用中點公式求出點P的縱坐標即可;
的中點利用中點公式求出點P的縱坐標即可;
(2)根據點P是拋物線的頂點設拋物線的解析式為![]() ,解方程組
,解方程組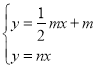 求出點A的坐標,再將點A的坐標代入拋物線的解析式即可求出a;
求出點A的坐標,再將點A的坐標代入拋物線的解析式即可求出a;
(3)由![]() 求出
求出![]() ,得到點
,得到點![]() 的坐標為
的坐標為![]() ,再分
,再分![]() 、
、![]() 兩種情況分別求出m的取值范圍.
兩種情況分別求出m的取值范圍.
(1)①∵![]() 與x軸交于點B,
與x軸交于點B,
∴當y=0時,得x=-2,
∴點B的坐標是(-2,0),
故答案為:![]() .
.
②∵直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,
,
∴當x=-1時,![]() =
=![]() ,
,
∴C(-1,![]() ),
),
∵直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,
,
∴當x=-1時,y=nx=-n,
∴D(-1,-n),
∴CD∥y軸,
∴點P的橫坐標是-1,縱坐標是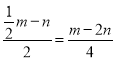 ,
,
故答案為:![]() .
.
(2)設拋物線的解析式為![]() .
.
![]() 直線
直線![]() :
:![]() 與直線
與直線![]() :
:![]() 交于點
交于點![]() ,
,
∴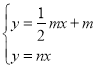 ,解得
,解得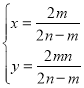 .
.
![]() 點
點![]() 的坐標是
的坐標是![]() .
.
![]() .
.
解得![]() .
.
(3)當![]() 時,
時,![]() .
.
![]() 拋物線解析式可以轉化為
拋物線解析式可以轉化為![]() .
.
![]() 點
點![]() 的坐標可以表示為
的坐標可以表示為![]() .
.
當![]() 時,拋物線開口向下,
時,拋物線開口向下,
![]() 當
當![]() 時,
時,![]() 有最大值,最大值為
有最大值,最大值為![]() .
.
![]() .解得
.解得![]() .
.
![]() .即
.即![]()
解得![]() .
.
當![]() 時,拋物線開口向上,
時,拋物線開口向上,
![]() 當
當![]() 時,
時,![]() 有最大值,最大值為
有最大值,最大值為![]() .
.
![]() .解得
.解得![]() .
.
![]() .即
.即![]() .
.
解得![]() .
.
綜上,![]() 的取值范圍是
的取值范圍是![]() 或
或![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案科目:初中數學 來源: 題型:
【題目】小字計劃在某外賣網站點如下表所示的菜品,已知每份訂單的配送費為3元,商家為了促銷,對每份訂單的總價(不含配送費)提供滿減優惠:滿30元減12元,滿60元減30元,滿100元減45元,如果小宇在購買下表中所有菜品時,采取適當的下訂單方式,那么他點餐的總費用最低可為___元.
菜品 | 單價(含包裝費) | 數量 |
| 30元 | 1 |
| 12元 | 1 |
| 30元 | 1 |
| 12元 | 1 |
| 3元 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,∠ACB=90°.
求作:射線CG,使得CG∥AB.
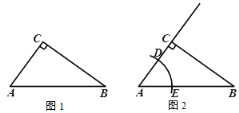
下面是小東設計的尺規作圖過程.
作法:
①以點A為圓心,適當長為半徑作弧,分別交AC,AB于D,E兩點;
②以點C為圓心,AD長為半徑作弧,交AC的延長線于點F;
③以點F為圓心,DE長為半徑作弧,兩弧在∠FCB內部交于點G;
④作射線CG.所以射線CG就是所求作的射線.
根據小東設計的尺規作圖過程,
(1)使用直尺和圓規,補全圖形;(保留作圖痕跡)
(2)完成下面的證明.
證明:連接FG、DE.
∵△ADE ≌ △_________,
∴∠DAE = ∠_________.
∴CG∥AB(___________________)(填推理的依據).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() ,以點
,以點![]() 為圓心,線段
為圓心,線段![]() 的長為半徑畫弧,與直線
的長為半徑畫弧,與直線![]() 位于第一象限的部分相交于點
位于第一象限的部分相交于點![]() ,則點
,則點![]() 的坐標為_______.
的坐標為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
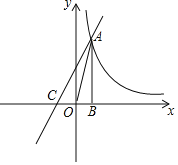
【題目】如圖,已知反比例函數y=![]() 的圖象經過第一象限內的一點A(n,4),過點A作AB⊥x軸于點B,且△AOB的面積為2.
的圖象經過第一象限內的一點A(n,4),過點A作AB⊥x軸于點B,且△AOB的面積為2.
(1)求m和n的值;
(2)若一次函數y=kx+2的圖象經過點A,并且與x軸相交于點C,求線段AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD⊥BC于點D,點F為AB上一點,連接CF,過點B作BE⊥BC交CF的延長線于點E,交AD于點H,且∠1=∠2
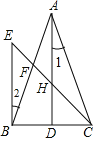
(1)求證:AB=AC;
(2)若∠1=22°,∠AFC=110°,求∠BCE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為改善辦學條件,計劃購進![]() 兩種規格的書架,經市場調查發現有線下和線上兩種方式,具有情況如下表:
兩種規格的書架,經市場調查發現有線下和線上兩種方式,具有情況如下表:
規格 | 線下 | 線上 | ||
單價(元/個) | 運費(元/個) | 單價(元/個) | 運費(元/個) | |
A | 240 | 0 | 210 | 20 |
B | 300 | 0 | 250 | 30 |
(Ⅰ)如果在線下購買![]() 兩種書架20個,共花費5520元,求
兩種書架20個,共花費5520元,求![]() 兩種書架各購買了多少個;
兩種書架各購買了多少個;
(Ⅱ)如果在線上購買![]() 兩種書架20個,共花費
兩種書架20個,共花費![]() 元,設其中
元,設其中![]() 種書架購買
種書架購買![]() 個,求W關于
個,求W關于![]() 的函數關系式;
的函數關系式;
(Ⅲ)在(Ⅱ)的條件下,若購買![]() 種書架的數量不少于
種書架的數量不少于![]() 種書架的2倍,請求出花費最少的購買方案,并計算按照該購買方案線上比線下節約多少錢.
種書架的2倍,請求出花費最少的購買方案,并計算按照該購買方案線上比線下節約多少錢.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 是線段
是線段![]() 上一點,
上一點,![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 的長為半徑作⊙
的長為半徑作⊙![]() ,過點
,過點![]() 作
作![]() 的垂線交⊙
的垂線交⊙![]() 于
于![]() ,
,![]() 兩點,點
兩點,點![]() 在線段
在線段![]() 的延長線上,連接
的延長線上,連接![]() 交⊙
交⊙![]() 于點
于點![]() ,以
,以![]() ,
,![]() 為邊作
為邊作![]() .
.

(1)求證:![]() 是⊙
是⊙![]() 的切線;
的切線;
(2)若![]() ,求四邊形
,求四邊形![]() 與⊙
與⊙![]() 重疊部分的面積;
重疊部分的面積;
(3)若![]() ,
,![]() ,連接
,連接![]() ,求
,求![]() 和
和![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com