
已知:如圖,點 在線段
在線段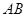 上,
上, 是等邊三角形.(1)當
是等邊三角形.(1)當 滿足怎樣的關系式時
滿足怎樣的關系式時 ;(2)當
;(2)當 時,求
時,求 的度數.
的度數.
(1)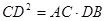 ;(2)
;(2)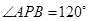
【解析】
試題分析:(1)先根據等邊三角形的性質可得PC=CD=PD,∠PCD=∠PDC=60°,即可得到∠PCA=∠PDB=120°,再有 ,即可證得結果.
,即可證得結果.
(2)由 可得∠A=∠DPB,再結合等邊三角形的性質即可求得結果.
可得∠A=∠DPB,再結合等邊三角形的性質即可求得結果.
(1)∵ 是等邊三角形
是等邊三角形
∴PC=CD=PD,∠PCD=∠PDC=∠CPD=60°
∴∠PCA=∠PDB=120°
∵ ,即
,即 ,
,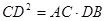
∴ ;
;
(2)∵ 時,
時,
∴∠A=∠DPB
∵∠PCD=∠A+∠APC=60°
∴∠DPB+∠APC=60°
∵∠CPD=60°
∴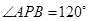 .
.
考點:等邊三角形的性質,相似三角形的判定和性質
點評:等邊三角形的判定和性質的應用是初中數學的重點和難點,與各個知識點的結合極為容易,因而是中考的熱點,尤其在壓軸題中極為常見,一般難度不大,需熟練掌握.


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案科目:初中數學 來源: 題型:
| ||
| 6 |

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
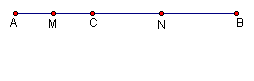
已知,如圖,點![]() 在線段
在線段![]() 上,且
上,且![]() ,
,![]() ,點
,點![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點.(1)求線段
的中點.(1)求線段![]() 的長度;
的長度;
(2)在(1)中,如果![]() ,
,![]() ,其它條件不變,你能猜測出
,其它條件不變,你能猜測出![]() 的長度嗎?請說出你發現的結論,并說明理由.
的長度嗎?請說出你發現的結論,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
已知:如圖,點![]() 為線段
為線段![]() 上一點,
上一點,![]() 、
、![]() 是等邊三角形,可以說明:
是等邊三角形,可以說明:![]() ≌
≌![]() ,從而得到結論:
,從而得到結論:![]() .現要求:
.現要求:
(1)將![]() 繞
繞![]() 點按逆時針方向旋轉180°,使
點按逆時針方向旋轉180°,使![]() 點落在
點落在![]() 上.請對照原題圖在下圖中畫出符合要求的圖形(不寫作法,保留作圖痕跡).
上.請對照原題圖在下圖中畫出符合要求的圖形(不寫作法,保留作圖痕跡).
(2)在(1)所得到的圖形中,結論“![]() ”是否還成立?若成立,請給予證明;若不成立,請說明理由.
”是否還成立?若成立,請給予證明;若不成立,請說明理由.
(3)在(1)所得到的圖形中,設![]() 的延長線與
的延長線與![]() 相交于
相交于![]() 點,請你判斷△ABD與四邊形
點,請你判斷△ABD與四邊形![]() 的形狀,并說明你的結論的正確性.
的形狀,并說明你的結論的正確性.
 | |||
 | |||
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com