
【題目】如圖,在△ABC中,AB=AC,AD是角平分線,BE平分∠ABC交AD于點E,點O在AB上,以OB為半徑的⊙O經過點E,交AB于點F 
(1)求證:AD是⊙O的切線;
(2)若AC=4,∠C=30°,求 ![]() 的長.
的長.
【答案】
(1)證明:
如圖,連接OE,
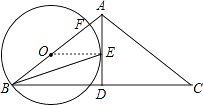
∵OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠EBD,
∴∠OEB=∠EBD,
∴OE∥BD,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠OEA=∠BDA=90°,
∴AD是⊙O的切線
(2)解:∵AB=AC=4,∠C=∠B=30°,
∴BD=2 ![]() ,
,
設圓的半徑為r,則BO=OE=r,AO=AC﹣OB=4﹣r,
∵OE∥BD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得r=8
,解得r=8 ![]() ﹣12,
﹣12,
∴ ![]() =
= ![]() =
= ![]()
【解析】(1)連接OE,利用角平分線的定義和圓的性質可得∠OBE=∠OEB=∠EBD,可證明OE∥BD,結合等腰三角形的性質可得AD⊥BD,可證得OE⊥AD,可證得AD為切線;(2)利用(1)的結論,結合條件可求得∠AOE=30°,由(1)可知OE∥BD,設半徑為r,則OB=OE=r,AO=4﹣r,在Rt△ABD中,由勾股定理可求得BD,由平行線分線段成比例可得到關于r的方程,可求得圓的半徑,利用弧長公式可求得 ![]() .
.
【考點精析】認真審題,首先需要了解等腰三角形的性質(等腰三角形的兩個底角相等(簡稱:等邊對等角)),還要掌握含30度角的直角三角形(在直角三角形中,如果一個銳角等于30°,那么它所對的直角邊等于斜邊的一半)的相關知識才是答題的關鍵.


 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】“一帶一路”是對古絲綢之路的傳承和提升,讓中國和世界的聯系更緊密,電氣設備是“一帶一路”沿線國家受青睞的商品。某企業計劃生產甲、乙兩種電氣設備出口,甲種設備售價50千元/件,乙種設備售價30千元/件,生產這兩種設備需要A、B兩種原料,生產甲設備需要A種原料4噸/件,B種原料2噸/件,生產乙設備需要A種原料3噸/件,B種原料1噸/件,已知A種原料有120噸,B種原料有50噸.
(1)如何安排生產,才能恰好使A、B兩種原料全部用完?此時總產值是多少千元?
(2)若使甲種設備售價上漲10%,而乙種設備售價下降10%,并且要求甲種設備比乙種設備多生產25件,問如何安排甲、乙兩種設備的生產,使銷售總產值能達到1375千元,此時A、B兩種原料還剩下多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先化簡,再求值:
(1)(9x3y-12xy3+3xy2)÷(-3xy)-(2y+x)(2y-x),其中x=1,y=-2;
(2)(m-n)(m+n)+(m+n)2-2m2,其中m、n滿足方程組![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
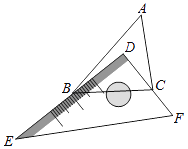
【題目】有一塊直角三角板DEF放置在△ABC上,三角板DEF的兩條直角邊DE、DF恰好分別經過點B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,AB∥CD,

求:(1)在圖(1)中∠B+∠D=?(2)在圖(2)中∠B+∠E1+∠D=?(3)在圖(3)中∠B+∠E1+∠E2+…+∠En﹣1+∠En+∠D=?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列計算正確的是( )
A.(x+y)2=x2+y2B.(﹣x+y)2=x2+2xy+y2
C.(x﹣2y)(x+2y)=x2﹣2y2D.(x﹣1)(﹣x﹣1)=1﹣x2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,第一次將△OAB變換成△OA1B1,第二次將△OA1B1變換成△OA2B2,第三次將△OA2B2變換成△OA3B3,已知A(1,5) 、A1(2,5) 、A2(4,5) 、A3(8,5) 、B(2,0) 、B1(4,0) 、B2(8,0) 、B3(16,0):若按此規律,將△OAB進行n次變換,得到△OAnBn。推測An的坐標是___________,Bn的坐標是___________。( )

A. (2n,5)(2n+1,0) B. (2n-1,5)(2n+1,0) C. (2n,5)(2n,0) D. (2n+1,5)(2n+1,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,EF//AD,![]() =
=![]() .說明:∠DGA+∠BAC=180°. 填空并寫出推理的依據.
.說明:∠DGA+∠BAC=180°. 填空并寫出推理的依據.

解:∵EF//AD,(已知)
∴![]() =__ __ (_____________________________)
=__ __ (_____________________________)![]()
又∵![]() =
=![]() , (已知)
, (已知)
∴![]() =__ _, (等量替代)
=__ _, (等量替代)
∴AB//___ ___, (_______________ _____________)
∴∠DGA+∠BAC=180° (_______________ _________)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先化簡,再求值:
(1)(1+a)(1-a)+(a-2)2,其中a=![]() ;
;
(2)(2x+3)(2x-3)-4x(x-1)+(x-2)2,其中x=-3.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com