
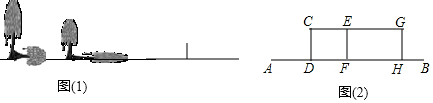
分析 A.(1)利用中心投影的定義畫圖;
(2)過點O作射線OB,交地面于點B;
B.(1)利用中心投影的定義畫圖;
(2)設小明原來的速度為xm/s,則CE=2xm,AM=AF-MF=(4x-1.2)m,EG=2×1.5x=3xm,BM=AB-AM=12-(4x-1.2)=13.2-4x,根據相似三角形的判定方法得到△OCE∽△OAM,△OEG∽△OMB,則$\frac{CE}{AM}=\frac{OE}{OM}$,$\frac{EG}{BM}$=$\frac{OE}{OM}$,$\frac{EG}{BM}$,即$\frac{2x}{4x-1.2}$=$\frac{3x}{13.2-4x}$,然后解方程解決.
解答 解:從A,B兩題中任選一題解答,我選擇A,
A.(1)如圖1,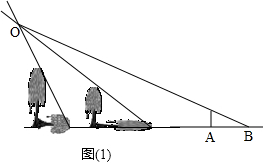
(2)如圖所示,線段AB即為所求線段;
故答案為:A.
B.(1)如圖2,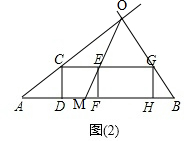
(2)設小明原來的速度為xm/s,則CE=2xm,AM=AF-MF=(4x-1.2)m,EG=2×1.5x=3xm,BM=AB-AM=12-(4x-1.2)=13.2-4x,
∵點C,E,G在一條直線上,CG∥AB,
∴△OCE∽△OAM,△OEG∽△OMB,
∴$\frac{CE}{AM}=\frac{OE}{OM}$,$\frac{EG}{BM}$=$\frac{OE}{OM}$,
∴$\frac{CE}{AM}$=$\frac{EG}{BM}$,即$\frac{2x}{4x-1.2}$=$\frac{3x}{13.2-4x}$,
解得x=1.5,
經檢驗x=1.5為方程的解,
∴小明原來的速度為1.5m/s,
故答案為:1.5m/s.
點評 本題考查了相似三角形的應用:從實際問題中抽象出幾何圖形,然后利用相似比計算相應線段的長.也考查了中心投影.


科目:初中數學 來源: 題型:解答題
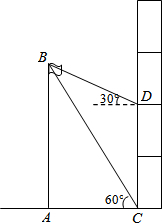 某校研究性學習小組測量學校旗桿AB的高度,如圖在教學樓一樓C處測得旗桿頂部的仰角為60°,在教學樓五樓D處測得旗桿頂部的仰角為30°,旗桿底部與教學樓一樓在同一水平線上,已知CD=12米,求旗桿AB的高度.
某校研究性學習小組測量學校旗桿AB的高度,如圖在教學樓一樓C處測得旗桿頂部的仰角為60°,在教學樓五樓D處測得旗桿頂部的仰角為30°,旗桿底部與教學樓一樓在同一水平線上,已知CD=12米,求旗桿AB的高度.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
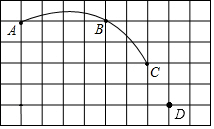 閱讀下面的材料,回答問題:
閱讀下面的材料,回答問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
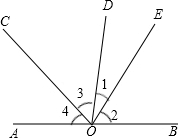 如圖,已知O為直線AB上一點,過點O向直線AB上方引三條射線OC、OD、OE,且OC平分∠AOD,∠BOE=3∠DOE,∠COE=70°.
如圖,已知O為直線AB上一點,過點O向直線AB上方引三條射線OC、OD、OE,且OC平分∠AOD,∠BOE=3∠DOE,∠COE=70°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com