【題目】二次函數y=ax2+bx+c的圖象如圖所示，下列結論：
①4ac＜b2；②a+c＞b；③2a+b＞0．
其中正確的有（ ）
A.①②
B.①③
C.②③
D.①②③
科目：初中數學 來源： 題型：
【題目】（1）如圖（1），在△ABC 中，∠BAC=70°，點 D 在 BC 的延長線上，三角形的內角∠ABC 與外角∠ACD 的角平分線 BP，CP 相交于點 P，求∠P 的度數.（寫出完整的解答過程）
（感知）：圖（1）中，若∠BAC=m°，那么∠P= °（用含有 m 的代數式表示）
（探究）：如圖（2）在四邊形 MNCB 中，設∠M=α，∠N＝β，α+β＞180°，四邊形的內角∠MBC與外角∠NCD 的角平分線 BP，CP 相交于點 P.為了探究∠P 的度數與 α 和 β 的關系，小明同學想到將這個問題轉化圖（1）的模型，因此，他延長了邊 BM 與 CN，設它們的交點為點 A， 如圖（ 3 ）， 則∠ A= （用含有 α 和 β 的代數式表示）， 因此∠P= ．（用含有 α 和 β 的代數式表示）
（拓展）：將（2）中的 α+β＞180°改為 α+β＜180°，四邊形的內角∠MBC 與外角∠NCD 的角平分線所在的直線相交于點 P，其它條件不變，請直接寫出∠P＝ ．（用 α，β的代數式表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在菱形ABCD中，∠ABC=60°，E是對角線AC上一點，F是線段BC延長線上一點，且CF=AE，連接BE、EF．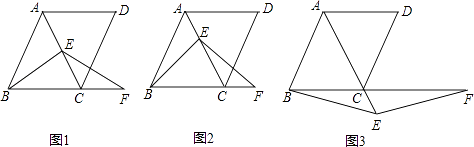
（1）若E是線段AC的中點，如圖1，易證：BE=EF（不需證明）；
（2）若E是線段AC或AC延長線上的任意一點，其它條件不變，如圖2、圖3，線段BE，EF有怎樣的數量關系，直接寫出你的猜想；并選擇一種情況給予證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】
朗讀者
自開播以來，以其厚重的文化底蘊和感人的人文情懷，感動了數以億計的觀眾，岳池縣某中學開展“朗讀”比賽活動，九年級
、
班根據初賽成績，各選出5名選手參加復賽，兩個班各選出的5名選手的復賽成績
滿分為100分
如圖所示．
平均數 | 中位數 | 眾數 | |
九 | 85 | 85 | |
九 | 80 |
根據圖示填寫表格；
結合兩班復賽成績的平均數和中位數，分析哪個班級的復賽成績較好；
如果規定成績較穩定班級勝出，你認為哪個班級能勝出？說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某物流公司引進A、B兩種機器人用來搬運某種貨物，這兩種機器人充滿電后可以連續搬運5小時，A種機器人于某日0時開始搬運，過了1小時，B種機器人也開始搬運，如圖，線段OG表示A種機器人的搬運量yA（千克）與時間x（時）的函數圖象，線段EF表示B種機器人的搬運量yB（千克）與時間x（時）的函數圖象．根據圖象提供的信息，解答下列問題：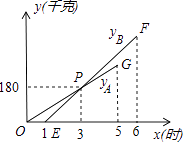
（1）求yB關于x的函數解析式；
（2）如果A、B兩種機器人連續搬運5個小時，那么B種機器人比A種機器人多搬運了多少千克？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2015年1月，市教育局在全市中小學中選取了63所學校從學生的思想品德、學業水平、學業負擔、身心發展和興趣特長五個維度進行了綜合評價．評價小組在選取的某中學七年級全體學生中隨機抽取了若干名學生進行問卷調查，了解他們每天在課外用于學習的時間，并繪制成如下不完整的統計圖．
根據上述信息，解答下列問題：
（1）本次抽取的學生人數是；扇形統計圖中的圓心角α等于；補全統計直方圖；
（2）被抽取的學生還要進行一次50米跑測試，每5人一組進行．在隨機分組時，小紅、小花兩名女生被分到同一個小組，請用列表法或畫樹狀圖求出她倆在抽道次時抽在相鄰兩道的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知在Rt△ABC中，∠C=90°，AD是∠BAC的角分線．
（1）以AB上的一點O為圓心，AD為弦在圖中作出⊙O．（不寫作法，保留作圖痕跡）；
（2）試判斷直線BC與⊙O的位置關系，并證明你的結論．
（3）若∠B=30°，計算S△DAC：S△ABC的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
