
【題目】如圖,在邊長為2的正方形![]() 中,
中,![]() 為
為![]() 的中點,
的中點,![]() 為邊
為邊![]() 上一動點,設
上一動點,設![]() ,線段
,線段![]() 的垂直平分線分別交邊
的垂直平分線分別交邊![]() 、
、![]() 于點
于點![]() 、
、![]() ,過
,過![]() 作
作![]() 于點
于點![]() ,過
,過![]() 作
作![]() 于點
于點![]() .
.
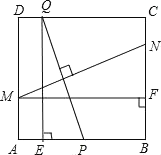
(1)當![]() 時,求證:
時,求證:![]() ;
;
(2)順次連接![]() 、
、![]() 、
、![]() 、
、![]() ,設四邊形
,設四邊形![]() 的面積為
的面積為![]() ,求出
,求出![]() 與自變量
與自變量![]() 之間的函數關系式,并求
之間的函數關系式,并求![]() 的最小值.
的最小值.
【答案】(1)見解析;(2)![]() ,
,![]() 的最小值為2
的最小值為2
【解析】
(1)由四邊形![]() 是正方形得到
是正方形得到![]() ,
,![]() ,又由
,又由![]() ,利用ASA即可證得;
,利用ASA即可證得;
(2)分為兩種情況:①當![]() 在
在![]() 上時,由點
上時,由點![]() 是邊
是邊![]() 的中點,
的中點,![]() ,
,![]() ,又由勾股定理求得
,又由勾股定理求得![]() ,由
,由![]() 得到
得到![]() 的值,又
的值,又![]() 求得面積
求得面積![]() ,由
,由![]() 范圍得到
范圍得到![]() 的最小值;②當
的最小值;②當![]() 在
在![]() 上時,同法可求
上時,同法可求![]() 的最小值.
的最小值.
解:(1)證明:∵四邊形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四邊形![]() 、
、![]() 都是矩形,
都是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴MF=QE
又∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
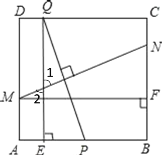
(2)解:分為兩種情況:①當![]() 在
在![]() 上時,
上時,
∵點![]() 是邊
是邊![]() 的中點,
的中點,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
由勾股定理,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵0≤AE≤AP
∴![]() ,
,
∴當![]() 時,
時,![]() .
.
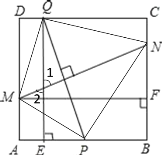
②當![]() 在
在![]() 上時,
上時,
∵點![]() 是邊
是邊![]() 的中點,
的中點,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
由勾股定理,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵AP≤AE≤AB
∴![]() ,
,
∴當![]() 時,
時,![]() .
.
綜上:![]() ,
,![]() 的最小值為2.
的最小值為2.


科目:初中數學 來源: 題型:
【題目】已知∠PAQ=36°,點B為射線AQ上一固定點,按以下步驟作圖:①分別以A,B為圓心,大于![]() AB的長為半徑畫弧,相交于兩點M,N;②作直線MN交射線AP 于點D,連接 BD;③以B為圓心,BA長為半徑畫弧,交射線AP 于點C; 根據以上作圖過程及所作圖形,下列結論中錯誤的是( )
AB的長為半徑畫弧,相交于兩點M,N;②作直線MN交射線AP 于點D,連接 BD;③以B為圓心,BA長為半徑畫弧,交射線AP 于點C; 根據以上作圖過程及所作圖形,下列結論中錯誤的是( )
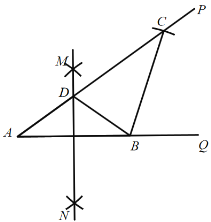
A.∠CDB=72°B.△ADB∽△ABCC.CD:AD=2:1D.∠ABC=3∠ACB
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前,步行已成為人們最喜愛的健身方式之一,通過手機可以計算行走的步數與相應的能量消耗.對比手機數據發現,小明步行消耗330000卡能量的步數與小紅步行消耗300000卡能量的步數相同.已知小明平均每步消耗的能量比小紅平均每步消耗的能量多3卡,求小紅平均每步消耗能量的卡數.
查看答案和解析>>
科目:初中數學 來源: 題型:
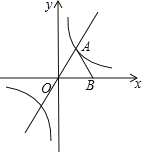
【題目】如圖所示,在平面直角坐標系中,等邊三角形OAB的一條邊OB在x軸的正半軸上,點A在雙曲線y=![]() (k≠0)上,其中點B為(2,0).
(k≠0)上,其中點B為(2,0).
(1)求k的值及點A的坐標
(2)△OAB沿直線OA平移,當點B恰好在雙曲線上時,求平移后點A的對應點A’的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx+c的對稱軸為直線x=﹣1,部分圖象如圖所示,下列判斷中:
①abc>0;
②b2﹣4ac>0;
③9a﹣3b+c=0;
④若點(﹣0.5,y1),(﹣2,y2)均在拋物線上,則y1>y2;
⑤5a﹣2b+c<0.
其中正確的個數有( )
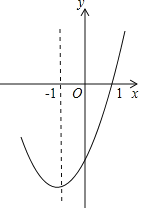
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
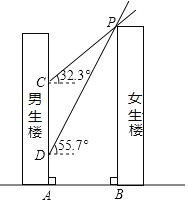
【題目】如圖,男生樓在女生樓的左側,兩樓高度均為90m,樓間距為AB,冬至日正午,太陽光線與水平面所成的角為![]() ,女生樓在男生樓墻面上的影高為CA;春分日正午,太陽光線與水平面所成的角為
,女生樓在男生樓墻面上的影高為CA;春分日正午,太陽光線與水平面所成的角為![]() ,女生樓在男生樓墻面上的影高為DA,已知
,女生樓在男生樓墻面上的影高為DA,已知![]() .
.
![]() 求樓間距AB;
求樓間距AB;
![]() 若男生樓共30層,層高均為3m,請通過計算說明多少層以下會受到擋光的影響?
若男生樓共30層,層高均為3m,請通過計算說明多少層以下會受到擋光的影響?![]() 參考數據:
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知線段AB=8,O為AB的中點,P是平面內的一個動點,在運動過程中保持OP=2不變,連結BP,將PB繞點P逆時針旋轉90°到PC,連結BC、AC,則線段AC長的最大值是_____.
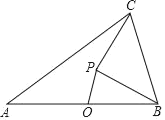
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形![]() 中
中![]() ,
,![]() 是
是![]() 的中點.請按要求完成下列作圖,
的中點.請按要求完成下列作圖,
①僅用無刻度直尺,不能用直尺中的直角;②保留作圖痕跡
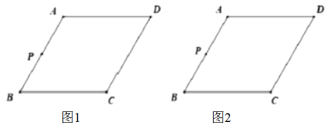
(1)在圖1中,過點![]() 作
作![]() 的平行線,與
的平行線,與![]() 交于點
交于點![]() .
.
(2)在圖2中,作線段![]() 的中垂線,垂足為點
的中垂線,垂足為點![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在平面直角坐標系中有兩點A(0,1),B(﹣1,0),動點P在反比例函數y=![]() 的圖象上運動,當線段PA與線段PB之差的絕對值最大時,點P的坐標為_____.
的圖象上運動,當線段PA與線段PB之差的絕對值最大時,點P的坐標為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com