
如圖,三角形ABC的兩個頂點B、C在圓上,頂點A在圓外,AB、AC分別交圓于E、D兩點,連結EC、BD.
(1)求證:ΔABD∽ΔACE;
(2)若ΔBEC與ΔBDC的面積相等,試判定三角形ABC的形狀.

(1)證明:因為![]() 弧ED所對的圓周角相等,所以∠EBD=∠ECD,…………………2分
弧ED所對的圓周角相等,所以∠EBD=∠ECD,…………………2分
又因為∠A=∠A,所以△A![]() BD∽ΔACE.……………………………………………4分
BD∽ΔACE.……………………………………………4分
(2)法1:因為S△BEC=S△BCD,
S△ACE=S△ABC-S△BEC,S△ABD=S△ABC一S△BCD,………………………………6分
所以S△ACE=S△ABD,
又由(1)知△ABD∽ΔACE,
所以對應邊之比等于1,……………………………………………………………8分
所以AB=AC,即三角形ABC為等腰三角形.……………………………………9分
法2:因為ΔBEC與ΔBCD的面積相等,有公共底邊BC,所以高相等,
即E、D兩點到BC距離相等,所以ED‖BC,……………………………………6分
所以∠BCE=∠CED,
又因為∠CED=∠CBD,
所以∠BCE=∠CBD,………………………………………………………………8分![]()
由(1)知△ABD∽ΔACE,
所以∠ABD=∠ACE,
所以∠ABC=∠ACB,
即三角形ABC為等腰三角形. ……………………………………………………9分


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:初中數學 來源: 題型:
 (2012•濰坊)如圖,三角形ABC的兩個頂點B、C在圓上,頂點A在圓外,AB、AC分別交圓于E、D兩點,連接EC、BD.
(2012•濰坊)如圖,三角形ABC的兩個頂點B、C在圓上,頂點A在圓外,AB、AC分別交圓于E、D兩點,連接EC、BD.查看答案和解析>>
科目:初中數學 來源: 題型:
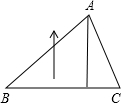 如圖,三角形ABC的底邊BC長3厘米,BC邊上的高是2厘米,將三角形以每秒3厘米的速度沿高的方向向上移動2秒,這時,三角形掃過的面積是多少平方厘米( )
如圖,三角形ABC的底邊BC長3厘米,BC邊上的高是2厘米,將三角形以每秒3厘米的速度沿高的方向向上移動2秒,這時,三角形掃過的面積是多少平方厘米( )| A、21 | B、19 | C、17 | D、15 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com