【題目】在
中，BD是它的一條對角線，過A、C兩點分別作
，
，E、F為垂足．
（1）如圖，求證：
；
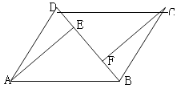
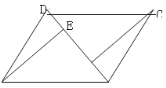
（2）如圖，連接AC，設AC、BD交于點O，若
．在不添加任何輔助線的情況下，請直接寫出圖中的所有長度是OE長度2倍的線段．
【答案】（1）見解析；（2）OA、OC、EF.
【解析】
（1）根據平行四邊形的AD∥BC，AB∥CD，AD=BC，AB=CD，根據平行線的性質得到∠ADE=∠CBF，由垂直的定義得到∠AEB=∠CFD=90°，根據全等三角形的性質即可得到結論；
（2）根據平行四邊形的性質得到AO=CO，根據直角三角形的性質即可得到結論．
（1）證明：∵四邊形ABCD是平行四邊形
∴
∴
∵
，
，
∴
在
和
中
∴
∴
（2）∵四邊形ABCD是平行四邊形，
∴AO=CO，
∵∠DOC=120°，
∴∠AOE=60°，
∴∠OAE=30°，
∴AO=2OE，
∴OC=2OE，
∵OD=OB，DE=BF，
∴OE=OF，
∴EF=2OE．
通城學典默寫能手系列答案科目：初中數學 來源： 題型：
【題目】已知：如圖，點C在AOB的一邊OA上，過點C的直線DE//OB，CF平分ACD，CG CF于C ．
（1）若O =40，求ECF的度數；
（2）求證：CG平分OCD；
（3）當O為多少度時，CD平分OCF，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖1，在正方形ABCD中，M是BC邊（不含端點B、C）上任意一點，P是BC延長線上一點，N是∠DCP的平分線上一點．若∠AMN＝90°，求證：AM＝MN．
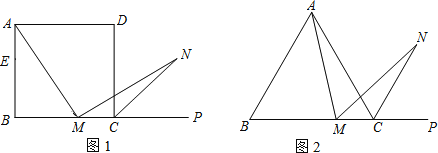
下面給出一種證明的思路，你可以按這一思路證明，也可以選擇另外的方法證明．
證明：在邊AB上截取AE＝MC，連接ME．正方形ABCD中，∠B＝∠BCD＝90°，AB＝BC．∴∠NMC＝180°﹣∠AMN﹣∠AMB＝180°﹣∠B﹣∠AMB＝∠MAB＝∠MAE．
（下面請你完成余下的證明過程）
（2）若將（1）中的“正方形ABCD”改為“正三角形ABC”（如圖2），N是∠ACP的平分線上一點，則∠AMN＝60°時，結論AM＝MN是否還成立？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】作圖題：在圖（1）（2）所示拋物線中，拋物線與
軸交于
、
，與
軸交于
，點
是拋物線的頂點，過平行于軸的直線是它的對稱軸，點
在對稱軸上運動。僅用無刻度的直尺畫線的方法，按要求完成下列作圖：
（1）在圖①中作出點，使線段
最小；
（2）在圖②中作出點，使線段
最大.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線C：y＝ax2－2ax＋c經過點C(1，2)，與x軸交于A(－1，0)、B兩點
(1) 求拋物線C的解析式
(2) 如圖1，直線
交拋物線C于S、T兩點，M為拋物線C上A、T之間的動點，過M點作ME⊥x軸于點E，MF⊥ST于點F，求ME＋MF的最大值
(3) 如圖2，平移拋物線C的頂點到原點得拋物線C1，直線l：y＝kx－2k－4交拋物線C1于P、Q兩點，在拋物線C1上存在一個定點D，使∠PDQ＝90°，求點D的坐標
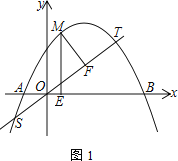
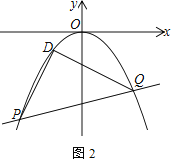
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖：在數軸上，點A表示a, 點B表示b, 點C表示c,b是最大的負整數，且a,c滿足
________，
_________，
_____________
若將數軸折疊，使得
點與
點重合，則點
與數____________表示的點重合；
點
開始在數軸上運動，若點以每秒
個單位長度的速度向左運動，同時，點和點分別以每秒
個單位長度和
個單位長度的速度向右運動，假設
秒鐘過后，
①請問:
的值是否隨著時間的變化而改變？若變化，請說明理由；若不變，請求其值．
②探究:若點
向右運動，點向左運動，速度保持不變，
的值是否隨著時間的變化而改變？若變化，請說明理由；若不變，請求其值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某中學開展“一起閱讀，共同成長”課外讀書周活動，活動后期隨機調查了八年級部分學生一周的課外閱讀時間，并將結果繪制成兩幅不完整的統計圖，請你根據統計圖的信息回答下列問題：
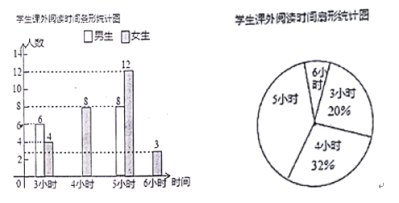
（1)本次調查的學生總數為______人，在扇形統計圖中，課外閱讀時間為5小時的扇形圓心角度數是______；
（2）請你補全條形統計圖；
（3）若全校八年級共有學生
人，估計八年級一周課外閱讀時間至少為
小時的學生有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某地的一座人行天橋如圖所示，天橋高為6米，坡面BC的坡度為1：1，為了方便行人推車過天橋，有關部門決定降低坡度，使新坡面的坡度為1：
．
（1）求新坡面的坡角∠CAB的度數；
（2）原天橋底部正前方8米處（PB的長）的文化墻PM是否需要拆除？請說明理由．
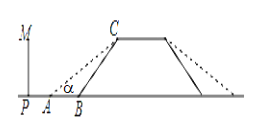
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】 某公園準備修建一塊長方形草坪，長為a米，寬為b米．并在草坪上修建如圖所示的十字路,
已知十字路寬2米.
（1）用含a、b的代數式表示修建的十字路的面積.
（2）若a=30，b=20，求草坪（陰影部分）的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com