
【題目】已知A、B兩地相距50單位長度。小李從A地出發去B地,以每分鐘2單位長度的速度行進,第一次他向左1單位長度,第二次他向右2單位長度,第三次再向左3單位長度,第四次又向右4單位長度,……,按此規律行進,如果A地在數軸上表示的數為-16.
(1)B地在數軸上表示的數為________________。
(2)若B地在原點的右側,經過第八次進行后,小李到達點P,此時點P與點B相距_____________單位長度,八次運動完成后一共經過__________分鐘。
(3)若經過n次(n為正整數)行進后,小李到達點Q,在數軸上點Q表示的數如何表示?(直接寫出結果)
【答案】(1)-66或34;(2)46,18;(3)n為奇數時,![]() ;n為偶數時,
;n為偶數時,![]()
【解析】
(1)由題意可得點B位于點A的左側或右側,AB兩地相距50單位長度,A地在數軸上表示的數為-16,可以得到B地在數軸上表示的數;
(2)根據題意可以發現奇數次運動和偶數次運動是有一定規律的,從而可以得到第八次行進后小李到達點P,此時點P與點B相距幾個單位長度和八次運動完成后一共經過了幾分;
(3)根據題意可以發現奇數次運動和偶數次運動是有一定規律的,從而可以寫出n為偶數和奇數時,在數軸上點Q表示的數是什么.
(1)∵AB兩地相距50單位長度,A地在數軸上表示的數為16,
∴點B表示的數為:1650=66或16+50=34,
即B地在數軸上表示的數是66或34;
(2)由題意可得,
第一次運動到點:161,
第二次為:161+2=16+1,
第三次為:16+13=162,
第四次為:162+4=16+2,
由上可得,第奇數次運動到點16![]() ,第偶數次運動到點:16+
,第偶數次運動到點:16+![]() ,
,
∴第八次運動到點P為:16+![]() =16+4=12,
=16+4=12,
∵B地在原點的右側,
∴點B表示的數為:34,
∴點P與點B相距的單位長度為:34(12)=46,
∴八次運動完成后經過的時間為:(1+2+3+4+5+6+7+8)÷2=36÷2=18(分鐘),
即B地在原點的右側,經過第八次行進后小李到達點P,此時點P與點B相距46個單位長度,八次運動完成后一共經過了18分鐘;
(3)由題意可得,
第一次運動到點:161,
第二次為:161+2=16+1,
第三次為:16+13=162,
第四次為:162+4=16+2,
由上可得,第奇數次運動到點16![]() ,第偶數次運動到點:16+
,第偶數次運動到點:16+![]() ,
,
即當n為奇數時,在數軸上點Q表示的數為:16![]() ;當n為偶數時,在數軸上點Q表示的數為:16+
;當n為偶數時,在數軸上點Q表示的數為:16+![]() .
.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
【題目】如圖是某公園的一角,∠AOB=90°,弧AB的半徑OA長是6m,C是OA的中點,點D在弧AB上,CD//OB,則圖中休閑區(陰影部分)的面積是( ) 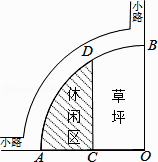
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O為直線AB上一點,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)請你數一數,圖中有多少個小于平角的角;
(2)求出∠BOD的度數;
(3)請通過計算說明OE是否平分∠BOC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,長方形OABC的邊OA在數軸上,O為原點,長方形OABC的面積為12,OC邊長為3.

(1)數軸上點A表示的數為________.
(2)將長方形OABC沿數軸水平移動,移動后的長方形記為O′A′B′C′,移動后的長方形O′A′B′C′與原長方形OABC重疊部分(如圖2中陰影部分)的面積記為S.
①當S恰好等于原長方形OABC面積的一半時,數軸上點A′表示的數是多少?
②設點A的移動距離AA′=x.
(ⅰ)當S=4時,求x的值;
(ⅱ)D為線段AA′的中點,點E在線段OO′上,且OE=![]() OO′,當點D,E所表示的數互為相反數時,求x的值.
OO′,當點D,E所表示的數互為相反數時,求x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(題文)如圖,在等腰直角三角形MNC中,CN=MN=![]() ,將△MNC繞點C順時針旋轉60°,得到△ABC,連接AM,BM,BM交AC于點O.
,將△MNC繞點C順時針旋轉60°,得到△ABC,連接AM,BM,BM交AC于點O.
(1)∠NCO的度數為________;
(2)求證:△CAM為等邊三角形;
(3)連接AN,求線段AN的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
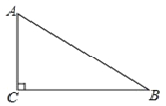
【題目】如圖,在 ABC ,C 90,AC<BC,D 為 BC 上一點,且到 A、B 兩點的距離相等.
(1)用直尺和圓規,作出點 D 的位置(不寫作法,保留作圖痕跡);
(2)連結 AD,若 B 36 ,求∠CAD 的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
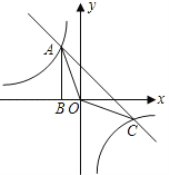
【題目】如圖,Rt△ABO的頂點A是雙曲線y1=![]() 與直線y2=-x-(k+1)在第二象限的交點.AB⊥x軸于B,且S△ABO=
與直線y2=-x-(k+1)在第二象限的交點.AB⊥x軸于B,且S△ABO=![]() .
.
(1)求這兩個函數的解析式;
(2)求△AOC的面積.
(3)直接寫出使y1>y2成立的x的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com