
【題目】已知:線段![]() .
.

(1)如圖1,點![]() 沿線段
沿線段![]() 自點
自點![]() 向
向![]() 點以
點以![]() 厘米
厘米![]() 秒運動,同時點
秒運動,同時點![]() 沿線段
沿線段![]() 自點
自點![]() 向
向![]() 點以
點以![]() 厘米
厘米![]() 秒運動,經過_________秒,
秒運動,經過_________秒,![]() 、
、![]() 兩點相遇.
兩點相遇.
(2)如圖1,點![]() 沿線段
沿線段![]() 自
自![]() 點向
點向![]() 點以
點以![]() 厘米
厘米![]() 秒運動,點
秒運動,點![]() 出發
出發![]() 秒后,點
秒后,點![]() 沿線段
沿線段![]() 自
自![]() 點向
點向![]() 點以
點以![]() 厘米
厘米![]() 秒運動,問再經過幾秒后
秒運動,問再經過幾秒后![]() 、
、![]() 相距
相距![]() ?
?
(3)如圖2:![]() ,
,![]() ,
,![]() ,點
,點![]() 繞著點
繞著點![]() 以
以![]() 度
度![]() 秒的速度逆時針旋轉一周停止,同時點
秒的速度逆時針旋轉一周停止,同時點![]() 沿直線
沿直線![]() 自
自![]() 點向
點向![]() 點運動,假若點
點運動,假若點![]() 、
、![]() 兩點能相遇,直接寫出點
兩點能相遇,直接寫出點![]() 運動的速度.
運動的速度.
【答案】(1)5;(2)3秒或5秒;(3)14cm或4.8cm.
【解析】
(1)根據點P、Q運動路程和等于AB求解;
(2)分點P與點Q在相遇前與相遇后相距6cm兩種情況列方程來解答;
(3)分P、Q在點O左右兩邊相遇來解答.
(1)30÷(2+4)=5(秒),
故答案為5;
(2)設再經過x秒后點P、Q兩點相距6cm.
當點P在點Q左邊時,2(x+3)+4x+6=30
解得x=3;
當點P在點Q右邊時,2(x+3)+4x-6=30
解得x=5,
所以再經過3或5秒后點P、Q兩點相距6cm;
(3)設點Q運動的速度為每秒xcm.
當P、Q兩點在點O左邊相遇時,[(180-60)÷60]x=30-2,
解得x=14;
當P、Q兩點在點O右邊相遇時,[(360-60)÷60]x=30-6,
解得x=4.8,
所以若P、Q兩點能相遇點Q運動的速度為每秒14cm或4.8cm.


科目:初中數學 來源: 題型:
【題目】已知:線段![]() .
.
(1)如圖1,點![]() 沿線段
沿線段![]() 自
自![]() 點向
點向![]() 點以
點以![]() 秒運動,同時點
秒運動,同時點![]() 沿線段
沿線段![]() 自
自![]() 點向
點向![]() 點以
點以![]() 秒運動.
秒運動.
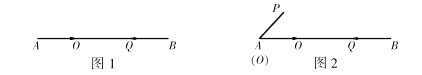
①問經過幾秒后![]() 相遇?
相遇?
②幾秒鐘后![]() 相距
相距![]() ?
?
(2)如圖2,![]() ,
,![]() ,點
,點![]() 以每秒
以每秒![]() 沿線段
沿線段![]() 自
自![]() 點向
點向![]() 點運動,同時點
點運動,同時點![]() 沿線段
沿線段![]() 自
自![]() 點向
點向![]() 點運動,點
點運動,點![]() 自
自![]() 點向
點向![]() 點運動的同時線段
點運動的同時線段![]() 以每秒
以每秒![]() 的速度繞點
的速度繞點![]() 順時針旋轉一周停止,假如
順時針旋轉一周停止,假如![]() 兩點能相遇,求點
兩點能相遇,求點![]() 運動的速度.
運動的速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線L與y=2x+1的交于點A(2,a),與直線y=x+2的交于點B(b,1)
(1)求a,b的值;
(2)求直線l的函數表達式;
(3)求直線L、x軸、直線y=2x+1圍成的圖形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠ABC ∠ACB ,BD 、CD 分別平分△ABC 的內角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延長線于點 E ,以下結論:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正確的結論有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正確的結論有( )
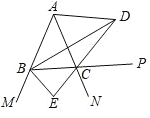
A.1 個B.2 個C.3 個D.4 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,用棋子擺成一組“上”字:

如果按照以上規律繼續擺下去,那么通過觀察,可以發現:
(1)第![]() 個、第
個、第![]() 個圖形中的“上”字分別需要用多少枚棋子?
個圖形中的“上”字分別需要用多少枚棋子?
(2)第![]() 個圖形中的“上”字需要用多少枚棋子?
個圖形中的“上”字需要用多少枚棋子?
(3)七(3)班有![]() 名同學,能否讓這
名同學,能否讓這![]() 名同學按照以上規律恰好站成一個“上”字?若能,請計算最下面一“橫”的學生數;若不能,請說明理由.
名同學按照以上規律恰好站成一個“上”字?若能,請計算最下面一“橫”的學生數;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD邊長為1,![]() ,
,![]() ,則有下列結論:①
,則有下列結論:①![]() ;②點C到EF的距離是2-1;③
;②點C到EF的距離是2-1;③![]() 的周長為2;④
的周長為2;④![]() ,其中正確的結論有( )
,其中正確的結論有( )
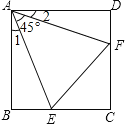
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是本地區一種產品30天的銷售圖象,圖1是產品日銷售量y(單位:件)與時間t(單位:天)的函數關系,圖2是一件產品的銷售利潤z(單位,元)與時間t(單位:天)的函數關系,已知日銷售利潤=日銷售量×一件產品的銷售利潤,下列正確結論的序號是____.

①第24天的銷售量為200件;
②第10天銷售一件產品的利潤是15元;
③第12天與第30天這兩天的日銷售利潤相等;
④第30天的日銷售利潤是750元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市經濟技術開發區某智能手機有限公司接到生產300萬部智能手機的訂單,為了盡快交貨,增開了一條生產線,實際每月生產能力比原計劃提高了50%,結果比原計劃提前5個月完成交貨,求每月實際生產智能手機多少萬部.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點A、B分別在射線OM、ON上運動(不與點O重合),AC、BC分別是∠BAO和∠ABO的角平分線,BC延長線交OM于點G.
(1)若∠MON=60°,則∠ACG= °;若∠MON=90°,則∠ACG= °;
(2)若∠MON=n°,請求出∠ACG的度數;(用含n的代數式表示)
(3)如圖2,若∠MON=n°,過C作直線與AB交于F,若CF∥OA時,求∠BGO-∠ACF的度數.(用含n的代數式表示).
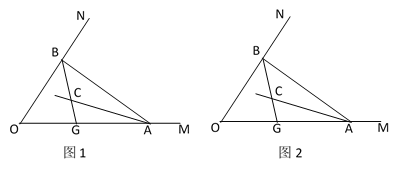
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com