
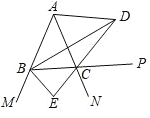
【題目】如圖,∠ABC ∠ACB ,BD 、CD 分別平分△ABC 的內角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延長線于點 E ,以下結論:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正確的結論有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正確的結論有( )
A.1 個B.2 個C.3 個D.4 個
【答案】D
【解析】
根據角平分線的定義、三角形的內角和定理、三角形的外角的性質、判斷即可.
① ∵BD、CD分別平分△ABC的內角∠ABC、外角∠ACP,
∴∠ACP=2∠DCP,∠ABC=2∠DBC,
又∵∠ACP=∠BAC+∠ABC,∠DCP=∠DBC+∠BDC,
∴∠BAC=2∠BDE,
∴BDE ![]() BAC
BAC
∴①正確;
②∵BD、BE分別平分△ABC的內角∠ABC、外角∠MBC,
∴∠DBE=∠DBC+∠EBC=![]() ∠ABC+
∠ABC+![]() ∠MBC=
∠MBC=![]() ×180°=90°,
×180°=90°,
∴EB⊥DB,
故②正確,
③∵∠DCP=∠BDC+∠CBD,2∠DCP=∠BAC+2∠DBC,∴2(∠BDC+∠CBD)=∠BAC+2∠DBC,
∴∠BDC=![]() ∠BAC,
∠BAC,
∵∠BAC+2∠ACB=180°,
∴![]() ∠BAC+∠ACB=90°,
∠BAC+∠ACB=90°,
∴∠BDC+∠ACB=90°,
故③正確,
④∵∠BEC=180°![]() (∠MBC+∠NCB)
(∠MBC+∠NCB)
=180°![]() (∠BAC+∠ACB+∠BAC+∠ABC)
(∠BAC+∠ACB+∠BAC+∠ABC)
=180°![]() (180°+∠BAC)
(180°+∠BAC)
∴∠BEC=90°![]() ∠BAC,
∠BAC,
∴∠BAC+2∠BEC=180°,故④正確,
即正確的有4個,
故選D


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】(問題情境)
如圖1,四邊形ABCD是正方形,M是BC邊上的一點,E是CD邊的中點,AE平分∠DAM.求證:AM=AD+MC.

(探究展示)
(2)若四邊形ABCD是長與寬不相等的矩形,其他條件不變,如圖2,試判斷AM=AD+MC是否成立?若成立,請給出證明,若不成立,請說明理由;
(拓展延伸)
(3)若(2)中矩形ABCD兩邊AB=6,BC=9,求AM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點A、B在數軸上分別表示數a、b,A、B之間的距離可表示為AB=|a﹣b|.已知數軸上A,B兩點分別表示有理數﹣1和x.
(1)若AB=4時,則x的值為 ;
(2)當x=7時,點A,B分別以每秒1個單位長度和2個單位長度的速度同時向數軸負方向運動.求經過多少秒后,點A到原點的距離是點B到原點的距離的2倍;
(3)如圖,點A,B,C,D四點在數軸上分別表示的數為﹣4,﹣1,2,6.是否存在點P在數軸上,使得點P到這四點的距離總和的最小?若存在,請直接寫點P的位置和距離總和的最小值.若不存在,請說明理由;
![]()
(4)某一直線沿街有2020戶民,假定相鄰兩戶居民間隔相同,分別記為a1,a2,a3,a4,a5,…,a2020.某餐飲公司想為這2020戶居民提供早餐,決定在路旁建立一個快餐店P.請問點P選在何處,才能使這2020戶居民到點P的距離總和最小?試說明原因.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一項工程,甲公司單獨做需要20天完成,乙公司單獨做所用時間是甲公司的1.5倍.
(1)若甲、乙兩公司合作完成這項工程需要多少天?
(2)若甲、乙兩公司合作完成這項工程,在第10天結束時,甲公司有別的任務,不能繼續合作,剩余部分由乙公司單獨完成,則乙公司還需要做幾天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:線段![]() .
.

(1)如圖1,點![]() 沿線段
沿線段![]() 自點
自點![]() 向
向![]() 點以
點以![]() 厘米
厘米![]() 秒運動,同時點
秒運動,同時點![]() 沿線段
沿線段![]() 自點
自點![]() 向
向![]() 點以
點以![]() 厘米
厘米![]() 秒運動,經過_________秒,
秒運動,經過_________秒,![]() 、
、![]() 兩點相遇.
兩點相遇.
(2)如圖1,點![]() 沿線段
沿線段![]() 自
自![]() 點向
點向![]() 點以
點以![]() 厘米
厘米![]() 秒運動,點
秒運動,點![]() 出發
出發![]() 秒后,點
秒后,點![]() 沿線段
沿線段![]() 自
自![]() 點向
點向![]() 點以
點以![]() 厘米
厘米![]() 秒運動,問再經過幾秒后
秒運動,問再經過幾秒后![]() 、
、![]() 相距
相距![]() ?
?
(3)如圖2:![]() ,
,![]() ,
,![]() ,點
,點![]() 繞著點
繞著點![]() 以
以![]() 度
度![]() 秒的速度逆時針旋轉一周停止,同時點
秒的速度逆時針旋轉一周停止,同時點![]() 沿直線
沿直線![]() 自
自![]() 點向
點向![]() 點運動,假若點
點運動,假若點![]() 、
、![]() 兩點能相遇,直接寫出點
兩點能相遇,直接寫出點![]() 運動的速度.
運動的速度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com