Question

在Rt△ABC中，∠C=90°，BC=4，AC=3，將△ABC繞著點B旋轉后點A落在直線BC上的點A′，點C落在點C′處，那么tan∠AA′C的值是    ．

Answer 1

【答案】分析：根據勾股定理求出AB的長度，然后分逆時針旋轉與順時針旋轉兩種情況求出A′C的長度，再根據正切值等于對邊比鄰邊列式計算即可得解．
解答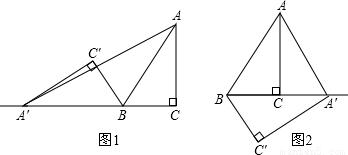：解：∵∠C=90°，BC=4，AC=3，
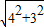
∴AB===5，
①如圖1，逆時針旋轉時，A′C=A′B+BC=5+4=9，
tan∠AA′C===，
②如圖2，順時針旋轉時，A′C=A′B-BC=5-4=1，
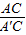
tan∠AA′C===3，
綜上，tan∠AA′C的值是3或．
故答案為：3或．
點評：本題考查了旋轉的性質，勾股定理的應用，銳角三角函數的定義，難點在于要分順時針與逆時針旋轉兩種情況討論．