
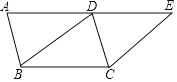
【題目】如圖,四邊形ABCD是平行四邊形,延長AD至點E,使DE=AD,連接BD.
(1)求證:四邊形BCED是平行四邊形;
(2)若DA=DB=2,cosA=![]() ,求點B到點E的距離.
,求點B到點E的距離.
【答案】(1)見解析;(2)BE=![]() .
.
【解析】
(1)根據平行四邊形的性質得到AD=BC,AD∥BC,等量代換得到DE=BC,DE∥BC,于是得到四邊形BCED是平行四邊形;
(2)連接BE,根據已知條件得到AD=BD=DE=2,根據直角三角形的判定定理得到∠ABE=90°,AE=4,解直角三角形即可得到結論.
(1)證明:∵四邊形ABCD是平行四邊形,
∴AD=BC,AD∥BC,
∵DE=AD,
∴DE=BC,DE∥BC,
∴四邊形BCED是平行四邊形;
(2)解:連接BE,
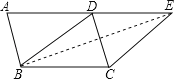
∵DA=DB=2,DE=AD,
∴AD=BD=DE=2,
∴∠ABE=90°,AE=4,
∵cosA=![]() ,
,
∴AB=1,
∴BE=![]() .
.


科目:初中數學 來源: 題型:
【題目】某校興趣小組以問卷調查的形式,隨機調查了某地居民對武漢封城后續措施的了解情況,設置了多選題,并將調查結果繪制成如圖不完整的統計圖.
選項 | A | B | C | D | E |
后續措施 | 擴大宣傳力度 | 分類隔離病人 | 封閉小區 | 聘請專業物資 | 采取其他措施 |
選擇人次 | 25 | 85 | 15 | 35 |
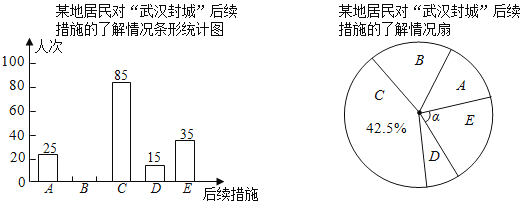
已知平均每人恰好選擇了兩個選項,根據以上信息回答下列問題:
(1)求參與本次問卷調查的居民人數,并補全條形統計圖;
(2)在扇形統計圖中,求E選項對應圓心角α的度數;
(3)根據此次調查結果估計該地100萬居民當中選擇D選項的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年豬肉價格受非洲豬瘟疫情影響,有較大幅度的上升,為了解某地區養殖戶受非洲豬瘟疫情感染受災情況,現從該地區建檔的養殖戶中隨機抽取了部分養殖戶進行了調查(把調查結果分為四個等級:A級:非常嚴重;B級:嚴重;C級:一般;D級:沒有感染),并將調查結果繪制成如下兩幅不完整的統計圖.請根據統計圖中的信息解決下列問題:
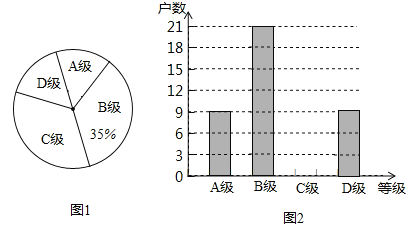
(1)本次抽樣調查的養殖戶的總戶數是 ;把圖2條形統計圖補充完整.
(2)若該地區建檔的養殖戶有1500戶,求非常嚴重與嚴重的養殖戶一共有多少戶?
(3)某調研單位想從5戶建檔養殖戶(分別記為a,b,c,d,e)中隨機選取兩戶,進一步跟蹤監測病毒傳播情況,請用列表或畫樹狀圖的方法求出選中養殖戶e的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
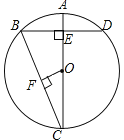
【題目】如圖,AC是⊙O的直徑,弦BD⊥AO于E,連接BC,過點O作OF⊥BC于F,若BD=8cm,AE=2cm,則OF的長度是( )
A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O中,AB是⊙O的直徑,G為弦AE的中點,連接OG并延長交⊙O于點D,連接BD交AE于點F,延長AE至點C,使得FC=BC,連接BC.
(1)求證:BC是⊙O的切線;
(2)⊙O的半徑為5,tanA=![]() ,求FD的長.
,求FD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將△ABC繞點A逆時針旋轉得到△ADE,其中點B、C分別與點D、E對應,如果B、D、C三點恰好在同一直線上,那么下列結論錯誤的是( )
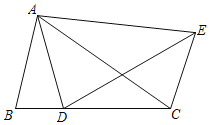
A.∠ACB=∠AEDB.∠BAD=∠CAE
C.∠ADE=∠ACED.∠DAC=∠CDE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.為了解全國中學生視力的情況,應采用普查的方式
B.某種彩票中獎的概率是![]() ,買1000張這種彩票一定會中獎
,買1000張這種彩票一定會中獎
C.從2000名學生中隨機抽取200名學生進行調查,樣本容量為200名學生
D.從只裝有白球和綠球的袋中任意摸出一個球,摸出黑球是確定事件
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四個全等的直角三角形按圖示方式圍成正方形ABCD,過各較長直角邊的中點作垂線,圍成面積為S的小正方形EFGH.已知AM為Rt△ABM較長直角邊,AM=2![]() EF,則正方形ABCD的面積為( )
EF,則正方形ABCD的面積為( )

A. 14SB. 13SC. 12SD. 11S
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(9分)在如圖的方格中,△OAB的頂點坐標分別為O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1與△OAB是關于點P為位似中心的位似圖形.

(1)在圖中標出位似中心P的位置,并寫出點的坐標及△O1A1B1與△OAB的相似比;
(2)以原點O為位似中心,在y軸的左側畫出△OAB的一個位似△OA2B2,使它與△OAB的位似比為2:1,并寫出點B的對應點B2的坐標;
(3)在(2)條件下,若點M(a,b)是△OAB邊上一點(不與頂點重合),寫出M在△OA2B2中的對應點M2的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com