
【題目】如圖,![]() 是
是![]() 的弦,
的弦,![]() 為半徑
為半徑![]() 的中點,過
的中點,過![]() 作
作![]() 交弦
交弦![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,且
,且![]() 是
是![]() 的切線.
的切線.
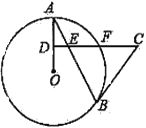
(1)求證:![]() ;
;
(2)連接![]() ,
,![]() ,求
,求![]() ;
;
(3)如果![]() ,
,![]() ,
,![]() ,求
,求![]() 的半徑.
的半徑.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() 的半徑為
的半徑為![]() .
.
【解析】
(1)連接OB,根據切線的性質得到![]() 根據等角的余角相等得到
根據等角的余角相等得到![]() 對頂角相等得到
對頂角相等得到![]() ,等量代換得到
,等量代換得到![]() 即可證明.
即可證明.
(2)連接OF,AF,BF,首先證明△OAF是等邊三角形,再利用圓周角定理:同弧所對的圓周角是所對圓心角的一半即可求出∠ABF的度數,即可求解.
(3)過點![]() 作
作![]() 于點
于點![]() ,根據等腰三角形的性質得到
,根據等腰三角形的性質得到![]() ,在
,在![]() 中,
中,![]() 設
設![]() ,
,![]() ,則
,則![]() ,證明
,證明![]() ,根據相似三角形的性質得到
,根據相似三角形的性質得到![]() 即
即![]() ,解得
,解得![]() ,求出
,求出![]() ,即可求出
,即可求出![]() 的半徑為
的半徑為![]() .
.
(1)證明:如圖,連接OB
∵![]()
∴![]()
∵![]() 切⊙O于
切⊙O于![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
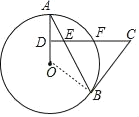
(2)解:連接![]() ,
,![]() ,
,![]()
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]() 是等邊三角形
是等邊三角形
∴![]()
∴![]()
∴![]()

(3)過點![]() 作
作![]() 于點
于點![]()
∵![]()
∴![]()
∵在![]() 中,
中,![]()
設![]() ,
,![]() ,則
,則![]()
∵![]() ,
,![]()
∴![]()
又∵![]()
∴![]()
∴![]() 即
即![]()
∴![]()
∴![]()
∴![]() 即
即![]() 的半徑為
的半徑為![]() .
.



 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:初中數學 來源: 題型:
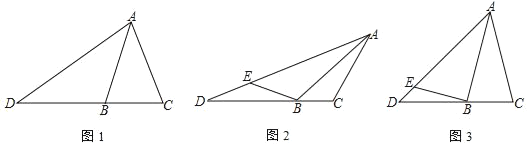
【題目】在△ABC中,D是CB延長線上一點,∠BAD=∠BAC.
(1)如圖,求證:![]() ;
;
(2)如圖,在AD上有一點E,∠EBA=∠ACB=120°.若AC=2BC=2,求DE的長;
(3)如圖,若AB=AC=2BC=4,BE⊥AB交AD于點E,直接寫出△BDE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市預測某飲料有發展前途,用1600元購進一批飲料,面市后果然供不應求,又用6000元購進這批飲料,第二批飲料的數量是第一批的3倍,但單價比第一批貴2元.
(1)第一批飲料進貨單價多少元?
(2)若二次購進飲料按同一價格銷售,兩批全部售完后,獲利不少于1200元,那么銷售單價至少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線y=![]() x+2與y軸交于點A,與雙曲線y=
x+2與y軸交于點A,與雙曲線y=![]() 有一個交點為B(2,3),將直線AB向下平移,與x軸.y軸分別交于點C,D,與雙曲線的一個交點為P,若
有一個交點為B(2,3),將直線AB向下平移,與x軸.y軸分別交于點C,D,與雙曲線的一個交點為P,若![]() ,則點D的坐標為________.
,則點D的坐標為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB、CD為兩個建筑物,建筑物AB的高度為100米,從建筑物AB的頂點A處測得建筑物CD的頂部C處的俯角∠EAC為30°,測得建筑物CD的底部D處的俯角∠EAD為45°.
(1)求兩建筑物底部之間水平距離BD的長度;
(2)求建筑物CD的高度(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:
我們知道,四邊形的一條對角線把這個四邊形分成了兩個三角形,如果這兩個三角形相似(不全等),我們就把這條對角線叫做這個四邊形的“相似對角線”.
理解:
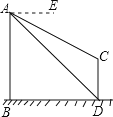
(1)如圖1,已知Rt△ABC在正方形網格中,請你只用無刻度的直尺在網格中找到一點D,使四邊形ABCD是以AC為“相似對角線”的四邊形(保留畫圖痕跡,找出3個即可);
(2)如圖2,在四邊形ABCD中,∠ABC=80°,∠ADC=140°,對角線BD平分∠ABC.
求證:BD是四邊形ABCD的“相似對角線”;
(3)如圖3,已知FH是四邊形EFCH的“相似對角線”,∠EFH=∠HFG=30°,連接EG,若△EFG的面積為2![]() ,求FH的長.
,求FH的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某市的一幢在建的樓,準備上市銷售,該樓前有一座裝有高壓線的鐵塔BC經過,市民想知道高壓線的電輻射對居住是否有影響,則需要測量該樓到鐵塔的水平距離DC的長以及鐵塔BC的高度.為了安全,不能直接測量鐵塔的高度.在該樓的樓頂A處測得鐵塔的塔B的仰角過![]() ,測得鐵塔的塔底C的俯角
,測得鐵塔的塔底C的俯角![]() ,該樓的高度
,該樓的高度![]() ,求鐵塔BC的高度(參考數據:
,求鐵塔BC的高度(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2013年四川綿陽12分)“低碳生活,綠色出行”,自行車正逐漸成為人們喜愛的交通工具.某運動商城的自行車銷售量自2013年起逐月增加,據統計,該商城1月份銷售自行車64輛,3月份銷售了100輛.
(1)若該商城前4個月的自行車銷量的月平均增長率相同,問該商城4月份賣出多少輛自行車?
(2)考慮到自行車需求不斷增加,該商城準備投入3萬元再購進一批兩種規格的自行車,已知A型車的進價為500元/輛,售價為700元/輛,B型車進價為1000元/輛,售價為1300元/輛.根據銷售經驗,A型車不少于B型車的2倍,但不超過B型車的2.8倍.假設所進車輛全部售完,為使利潤最大,該商城應如何進貨?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com