
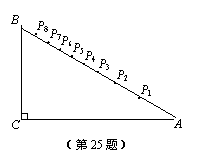
小明設計了一個“簡易量角器”:如圖,在△ABC中,∠C=90°,∠A=30°,CA=30 cm,在AB邊上有一系列點P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.
(1)求P3A的長(結果保留根號);
(2)求P5A的長(結果精確到1 cm,參考數據:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20,![]() ≈1.7);
≈1.7);
(3)小明發現P1,P2,P3…P8這些點中,相鄰兩點距離都不相同,于是計劃用含45°的直角三角形重新制作“簡易量角器”,結果會怎樣呢?請你幫他繼續探究.
 |
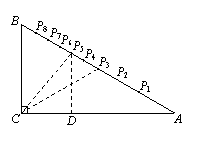
解:(1)連接P3C.
∵∠P3CA=∠A,∴P3C=P3A.
又∵∠P3CB=∠BCA-∠P3CA=60°![]() ,且∠B=∠BCA-∠A=60°,
,且∠B=∠BCA-∠A=60°,
 ∴∠P3CB=∠B,∴P3C=P3B,
∴∠P3CB=∠B,∴P3C=P3B,
∴P3A=P3B=![]() AB.
AB.
在Rt△ABC中,cos∠A=![]() ,
,
∴AB=![]() =20
=20![]() cm.
cm.
∴P3A=![]() AB=10
AB=10![]() cm. ……………………………………………3分
cm. ……………………………………………3分
(2)連接P5C,作P5D⊥CA,垂足為D.
由題意得,∠P5CA=50°,設CD=x cm.
在Rt△P5DC中,tan∠P5CD=![]() ,∴P5D=CD·tan∠P5CD=1.2x.
,∴P5D=CD·tan∠P5CD=1.2x.
在Rt△P5DA中,tan∠A=![]() ,∴DA=
,∴DA=![]() =1.2
=1.2![]() x.
x.
∵CA=30 cm,∴CD+DA=30 cm.
∴x+1.2![]() x=30.∴x=
x=30.∴x=![]() .
.
在Rt△P5DA中,sin∠A=![]() ,∴P5A=
,∴P5A=![]() =2.4x.
=2.4x.
∴P5A=2.4×![]() ≈24 cm.………………………………………7分
≈24 cm.………………………………………7分
(3)如圖,在△ABC中,∠C=90°,∠A=45°.
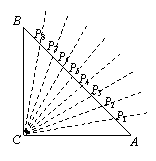 當P1,P2,P3…P8在斜邊上時.
當P1,P2,P3…P8在斜邊上時.
∵∠B=90°-∠A=45°,
∴∠B=∠A,∴AC=BC.
在△P1CA和△P8CB中,
∵∠P1CA=∠P8CB,AC=BC,∠A=∠B,
∴△P1CA≌△P8CB.∴P1A=P8B.
同理可得P2A=P7B,P3A=P6B,P4A=P5B.
則P1P2=P8P7,P2P3=P7P6,P3P4=P6P5.
在P1,P2,P3…P8這些點中,有三對相鄰點距離相等.
(回答“當P1,P2,P3…P8在直角邊上時,P1,P2,P3…P8這些點中,相鄰兩點距離都不同相”,得1分,根據等腰三角形軸對稱性直接得出結論,得2分)………………………………………………………10分


科目:初中數學 來源: 題型:
 (2013•玄武區一模)小明設計了一個“簡易量角器”:如圖,在△ABC中,∠C=90°,∠A=30°,CA=30cm,在AB邊上有一系列點P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.
(2013•玄武區一模)小明設計了一個“簡易量角器”:如圖,在△ABC中,∠C=90°,∠A=30°,CA=30cm,在AB邊上有一系列點P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.| 3 |
查看答案和解析>>
科目:初中數學 來源:2013年江蘇省南京市玄武區中考一模數學試卷(帶解析) 題型:解答題
小明設計了一個“簡易量角器”:如圖,在△ABC中,∠C=90°,∠A=30°,CA=30 cm,在AB邊上有一系列點P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.
(1)求P3A的長(結果保留根號);
(2)求P5A的長(結果精確到1 cm,參考數據:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20,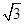 ≈1.7);
≈1.7);
(3)小明發現P1,P2,P3…P8這些點中,相鄰兩點距離都不相同,于是計劃用含45°的直角三角形重新制作“簡易量角器”,結果會怎樣呢?請你幫他繼續探究.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
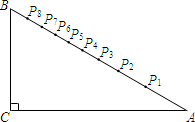 小明設計了一個“簡易量角器”:如圖,在△ABC中,∠C=90°,∠A=30°,CA=30cm,在AB邊上有一系列點P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.
小明設計了一個“簡易量角器”:如圖,在△ABC中,∠C=90°,∠A=30°,CA=30cm,在AB邊上有一系列點P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°. ≈1.7);
≈1.7);查看答案和解析>>
科目:初中數學 來源:2013年江蘇省南京市玄武區中考數學一模試卷(解析版) 題型:解答題
 ≈1.7);
≈1.7);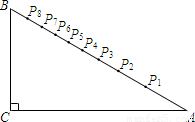
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com