Question

順次連接矩形各邊中點所得的四邊形（ ）
A．是軸對稱圖形而不是中心對稱圖形
B．是中心對稱圖形而不是軸對稱圖形
C．既是軸對稱圖形又是中心對稱圖形
D．沒有對稱性

Answer 1

【答案】分析：先判斷所得的四邊形的形狀，再判斷其對稱性．
解答：解：根據順次連接對角線相等的四邊形各邊中點所得四邊形是菱形，因為矩形的對角線相等，所以該四邊形是菱形．
所以它既是軸對稱圖形又是中心對稱圖形．故選C．
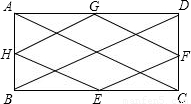
下面給予證明：
∵H、G為矩形ABCD的兩邊AB、AD的中點，
∴HG為△ABD的中位線，
∴HG=BD，
同理，EF=BD，FG=AC，HE=AC，
又∵AC=BD，
∴HG=HE=EF=GF，
∴四邊形HEFG為菱形．
點評：能夠根據三角形的中位線定理證明：順次連接對角線相等的四邊形各邊中點所得四邊形是菱形．了解特殊四邊形的對稱性．