
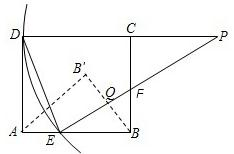
 時,△AB′B與△BEF是否相似?若相似,請加以證明;若不相似,簡要說明理由.
時,△AB′B與△BEF是否相似?若相似,請加以證明;若不相似,簡要說明理由.
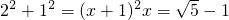 (負數舍去).
(負數舍去).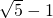 .
.
 ;
;
 ,
,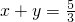 ,
,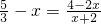 ,
, .
.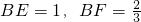 ;
; ,BB'=
,BB'= .
.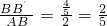 ,
,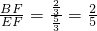 ,
,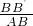 =
= ,
,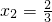 時,
時, .
.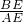 =
=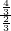 =2,
=2,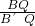 =1,
=1, ,AE=1時,△AB'B∽△BEF;
,AE=1時,△AB'B∽△BEF; ,
, 時,△AB'B與△BEF不相似.
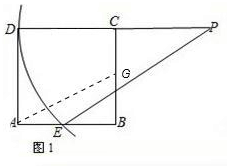
時,△AB'B與△BEF不相似. BC,進而可在Rt△ABG中,由勾股定理求得AE的長.
BC,進而可在Rt△ABG中,由勾股定理求得AE的長. 時,x+y=
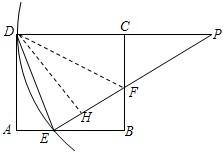
時,x+y= ,聯立(2)的函數關系式可求得此時x的值,進而可求出AE、BF的長;根據折疊的性質知:EF垂直平分BB′,設垂足為Q;在Rt△BEF中,根據直角三角形面積的不同表示方法,可求得BQ的長,也就得出了BB′的長;然后再判斷兩個直角三角形的對應邊是否成比例即可.
,聯立(2)的函數關系式可求得此時x的值,進而可求出AE、BF的長;根據折疊的性質知:EF垂直平分BB′,設垂足為Q;在Rt△BEF中,根據直角三角形面積的不同表示方法,可求得BQ的長,也就得出了BB′的長;然后再判斷兩個直角三角形的對應邊是否成比例即可.

 階梯計算系列答案
階梯計算系列答案科目:初中數學 來源: 題型:
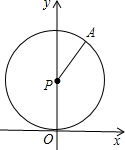 已知:如圖,⊙P與x軸切于點O,點P的坐標為(0,1),點A在⊙P上,且在第一象限,∠APO=150°,⊙P沿x軸正方向滾動,當點A第一次落在x軸上時,點P的坐標為
已知:如圖,⊙P與x軸切于點O,點P的坐標為(0,1),點A在⊙P上,且在第一象限,∠APO=150°,⊙P沿x軸正方向滾動,當點A第一次落在x軸上時,點P的坐標為查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 | 4 |
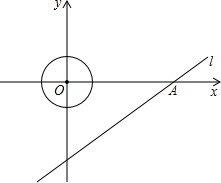 .5個單位/秒的速度運動,問在整個運動的過程中,點P在動圓的園面(圓上和圓的內部)上一共運動了多長時間?
.5個單位/秒的速度運動,問在整個運動的過程中,點P在動圓的園面(圓上和圓的內部)上一共運動了多長時間?查看答案和解析>>
科目:初中數學 來源: 題型:
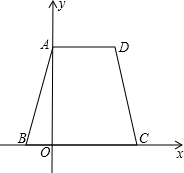 B=2
B=2| 10 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
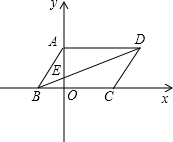 點E,AB=
點E,AB=| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
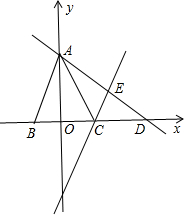 將△AOC沿直線AC折疊,點O落在平面內的點E處,直線AE交x軸于點D.
將△AOC沿直線AC折疊,點O落在平面內的點E處,直線AE交x軸于點D.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com