
【題目】甲乙兩人依次測量同一圓柱體工件的橫截面直徑(單位:![]() ),測得的數據分別如表1、表2.
),測得的數據分別如表1、表2.
表1:甲的測量數據
測量數據 | 9.8 | 9.9 | 10 | 10.1 | 10.3 |
頻數 | 1 | 3 | 3 | 2 | 1 |
表2:乙的測量數據
測量數據 | 9.7 | 9.8 | 10 | 10.1 | 10.3 |
頻數 | 1 | 2 | 3 | 2 | 2 |
(1)如果在這些測量數據中選擇一個數據作為工件直徑的估計值,應該是那個數據?請說明理由.
(2)如果甲再測量一次,求他測量出的數據恰好是估計值的概率;
(3)請直接判斷甲乙兩人誰的測量技術更好______(填甲或乙),你選擇的統計量是_______.
【答案】(1)應該是10,理由見解析;(2)![]() ;(3)甲,方差.
;(3)甲,方差.
【解析】
(1)把甲乙測量數據的平均值計算出來,即可得到估算值;
(2)根據甲測量的數據,用頻率估算概率,把測到10的概率估算出來即可得到答案;
(3)分別計算甲乙的方差,根據方差越小數據越穩定,進行比較即可得到答案;
解:(1)我選擇10作為估算值,理由如下:
甲測量的數據的平均值為:![]() ,
,
乙測量的數據的平均值為:![]() ,
,
甲乙測量數據的平均值都是10,
故我選擇10作為工件直徑的估計值;
(2)根據表一的數據,得到甲測量到10的頻率為:![]() ,
,
故用頻率估算概率,得到甲再測量一次,求他測量出的數據恰好是估計值的概率為![]() ;
;
(3)甲測量技術好,理由如下:
甲測量數據的方差為:
![]()
甲測量數據的方差為:
![]()
因此甲的方差小于乙的方差,故甲測量的數據比較穩定,
故我覺得甲測量技術更好;
故答案為:甲,方差;


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點A的坐標為
中,點A的坐標為![]() ,點B的坐標為
,點B的坐標為![]() ,拋物線
,拋物線![]() 的頂點為C.
的頂點為C.
(1)若拋物線經過點B時,求頂點C的坐標;
(2)若拋物線與線段![]() 恰有一個公共點,結合函數圖象,求a的取值范圍;
恰有一個公共點,結合函數圖象,求a的取值范圍;
(3)若滿足不等式![]() 的x的最大值為3,直接寫出實數a的值.
的x的最大值為3,直接寫出實數a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級有學生400人,為了解這個年級普及安全教育的情況,隨機抽取了20名學生,進行安全教育考試,測試成績(百分制)如下:
71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
(1)請補全七年級20名學生安全教育測試成績頻數分布直方圖;
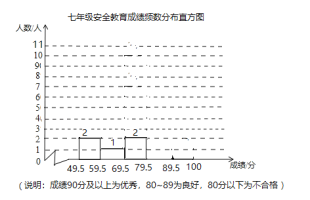
(2)樣本數據的平均數、中位數、眾數、優秀率如下表所示,請補充完整;
年級 | 平均數 | 中位數 | 眾數 | 優秀率 |
七年級 | 85.4 |
|
|
|
(3)估計七年級成績優秀的學生人數約為_________人.
(4)學校有安全教育老師男女各2名,現從這4名老師中隨機挑選2名參加“安全教育”宣傳活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小明同學設計的“過直線外一點作已知直線的平行線“的尺規作圖過程.

已知:如圖,直線![]() 和直線
和直線![]() 外一點
外一點![]() .
.
求作:直線![]() ,使直線
,使直線![]() 直線
直線![]() .
.
作法:如圖,
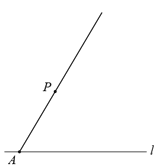
①在直線![]() 上任取一點
上任取一點![]() ,作射線
,作射線![]() ;
;
②以![]() 為圓心,
為圓心,![]() 為半徑作弧,交直線
為半徑作弧,交直線![]() 于點
于點![]() ,連接
,連接![]() ;
;
③以![]() 為圓心,
為圓心,![]() 長為半徑作弧,交射線
長為半徑作弧,交射線![]() 于點
于點![]() ;分別以
;分別以![]() 為圓心,大于
為圓心,大于![]() 長為半徑作弧,在
長為半徑作弧,在![]() 的右側兩弧交于點
的右側兩弧交于點![]() ;
;
④作直線![]() ;
;
所以直線![]() 就是所求作的直線.
就是所求作的直線.
根據上述作圖過程,回答問題:
(1)用直尺和圓規,補全圖中的圖形;
(2)完成下面的證明:
證明:由作圖可知![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() .(_______________________________)(填依據1).
.(_______________________________)(填依據1).
![]() ,
,
![]() .
.
![]() ,∴直線
,∴直線![]() 直線
直線![]() .(______________________)(填依據2).
.(______________________)(填依據2).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,存在半徑為2,圓心為(0,2)的
中,存在半徑為2,圓心為(0,2)的![]() ,點
,點![]() 為
為![]() 上的任意一點,線段
上的任意一點,線段![]() 繞點
繞點![]() 逆時針旋轉90°得到線段
逆時針旋轉90°得到線段![]() ,如果點
,如果點![]() 在線段
在線段![]() 上,那么稱點
上,那么稱點![]() 為
為![]() 的“限距點”.
的“限距點”.
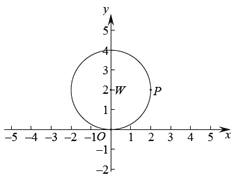
(1)在點![]() 中,
中,![]() 的“限距點”為____________________________;
的“限距點”為____________________________;
(2)如果過點![]() 且平行于
且平行于![]() 軸的直線
軸的直線![]() 上始終存在
上始終存在![]() 的“限距點”,畫出示意圖并直接寫出
的“限距點”,畫出示意圖并直接寫出![]() 的取值范圍;
的取值范圍;
(3)![]() 的圓心為
的圓心為![]() ,半徑為1,如果
,半徑為1,如果![]() 上始終存在
上始終存在![]() 的“限距點”,請直接寫出
的“限距點”,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市教育行政部門為了解初中學生參加綜合實踐活動的情況,隨機抽取了本市初一、初二、初三年級各![]() 名學生進行了調查,調查結果如圖所示,請你根據圖中的信息回答問題.
名學生進行了調查,調查結果如圖所示,請你根據圖中的信息回答問題.

(1)在被調查的學生中,參加綜合實踐活動的有多少人,參加科技活動的有多少人;
(2)如果本市有![]() 萬名初中學生,請你估計參加科技活動的學生約有多少名.
萬名初中學生,請你估計參加科技活動的學生約有多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解學生的安全意識,在全校范圍內隨機抽取部分學生進行問卷調查.根據調查結果,把學生的安全意識分成“淡薄”、“一般”、“較強”、“很強”四個層次,并繪制如下兩幅尚不完整的統計圖.
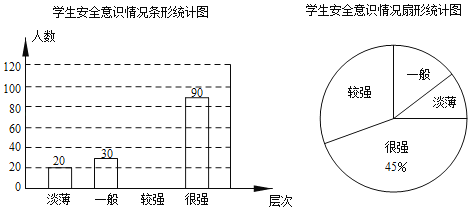
根據以上信息,解答下列問題:
(1)這次調查一共抽取了 名學生,將條形統計圖補充完整;
(2)扇形統計圖中,“較強”層次所占圓心角的大小為 °;
(3)若該校有1900名學生,現要對安全意識為“淡薄”、“一般”的學生強化安全教育,根據調查結果,請你估計全校需要強化安全教育的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 經過點
經過點![]() ,與
,與![]() 軸交于
軸交于![]() 兩點,
兩點,![]() 為頂點,
為頂點,![]() 為拋物線上一動點(與點
為拋物線上一動點(與點![]() 不重合)
不重合)
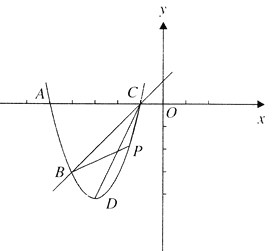
![]() 求該拋物線的解析式;
求該拋物線的解析式;
![]() 當點
當點![]() 在直線
在直線![]() 的下方運動時,求
的下方運動時,求![]() 的面積的最大值;
的面積的最大值;
![]() 該拋物線上是否存在點
該拋物線上是否存在點![]() ,使
,使![]() ?若存在,求出所有點
?若存在,求出所有點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織了2000名學生參加“愛我中華”知識競賽活動,為了了解本次知識競賽的成績分布情況,從中抽取了部分學生的得分進行統計:
成績 | 頻數 | 頻率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
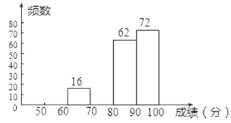
請你根據以上的信息,回答下列問題:
(1)![]() ,
,![]() ;
;
(2)在扇形統計圖中,“成績![]() 滿足
滿足![]() ”對應扇形的圓心角的度數是 ;
”對應扇形的圓心角的度數是 ;
(3)若將得分轉化為等級,規定:![]() 評為
評為![]() ,
,![]() 評為
評為![]() ,
,![]() 評為
評為![]() ,
,![]() 評為
評為![]() .這次全校參加競賽的學生約有 人參賽成績被評為“
.這次全校參加競賽的學生約有 人參賽成績被評為“![]() ”.
”.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com