
【題目】如圖,在平面直角坐標系![]() 中,存在半徑為2,圓心為(0,2)的
中,存在半徑為2,圓心為(0,2)的![]() ,點
,點![]() 為
為![]() 上的任意一點,線段
上的任意一點,線段![]() 繞點
繞點![]() 逆時針旋轉90°得到線段
逆時針旋轉90°得到線段![]() ,如果點
,如果點![]() 在線段
在線段![]() 上,那么稱點
上,那么稱點![]() 為
為![]() 的“限距點”.
的“限距點”.
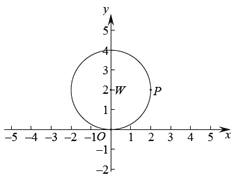
(1)在點![]() 中,
中,![]() 的“限距點”為____________________________;
的“限距點”為____________________________;
(2)如果過點![]() 且平行于
且平行于![]() 軸的直線
軸的直線![]() 上始終存在
上始終存在![]() 的“限距點”,畫出示意圖并直接寫出
的“限距點”,畫出示意圖并直接寫出![]() 的取值范圍;
的取值范圍;
(3)![]() 的圓心為
的圓心為![]() ,半徑為1,如果
,半徑為1,如果![]() 上始終存在
上始終存在![]() 的“限距點”,請直接寫出
的“限距點”,請直接寫出![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)分兩種情況:當![]() 軸時,
軸時,![]() 相切于
相切于![]() 軸時,分別作出相應圖形即可判斷;
軸時,分別作出相應圖形即可判斷;
(2)以![]() 為圓心,
為圓心,![]() 為半徑作圓,如果過點
為半徑作圓,如果過點![]() 且平行于
且平行于![]() 軸的直線
軸的直線![]() 上始終存在
上始終存在![]() 的“限距點”,則
的“限距點”,則![]() 在平行于
在平行于![]() 軸并相切于
軸并相切于![]() 的范圍內,據此求解即可;
的范圍內,據此求解即可;
(3)如果![]() 上始終存在
上始終存在![]() 的“限距點”,則
的“限距點”,則![]() 相切于
相切于![]() 和
和![]() ,據此求解即可.
,據此求解即可.
解:(1)如圖所示,
當![]() 軸時,
軸時,![]() 點的坐標為(4,0),
點的坐標為(4,0),
![]() 相切于
相切于![]() 軸時,
軸時,![]() 點的坐標為(0,4),
點的坐標為(0,4),
∴在點![]() 中,
中,![]() 的“限距點”為
的“限距點”為![]() ,
,![]() ,
,
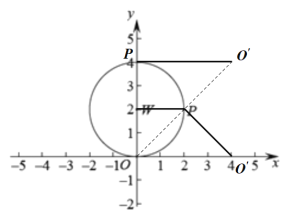
(2)如圖所示,以![]() 為圓心,
為圓心,![]() 為半徑作圓,過
為半徑作圓,過![]() 點作垂直于
點作垂直于![]() 軸的直線交
軸的直線交![]() 于
于![]() ,
,![]() 兩點,
兩點,
則,過![]() ,
,![]() 兩點并相切于
兩點并相切于![]() ,且平行于
,且平行于![]() 軸的直線
軸的直線![]() 上始終存在
上始終存在![]() 的“限距點”,
的“限距點”,
∴![]() ,
,
∴![]() 點坐標為:(2,
點坐標為:(2,![]() ),
),![]() 點坐標為:(2,
點坐標為:(2,![]() ),
),
∴![]() 的取值范圍是:
的取值范圍是:![]() ;
;
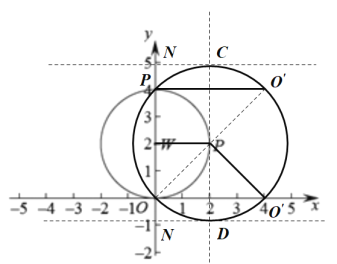
(3)如圖示,當![]() 的位置如圖所示時,
的位置如圖所示時, ![]() 上始終存在
上始終存在![]() 的“限距點”,
的“限距點”,
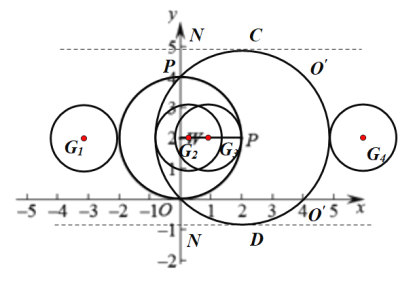
則,![]() 點坐標為:(-3,2),
點坐標為:(-3,2),
![]() 點坐標為:(
點坐標為:(![]() ,2),
,2),
![]() 點坐標為:(1,2),
點坐標為:(1,2),
![]() 點坐標為:(
點坐標為:(![]() ,2),
,2),
∴![]() 的取值范圍是:
的取值范圍是:![]() 或
或![]() .
.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
【題目】某快餐店外賣促銷,佳佳和點點想點外賣,每單需支付送餐費5元,每種餐食外賣價格如下表:
餐食種類 | 價格(單位:元) |
漢堡套餐 | 40 |
雞翅 | 16 |
雞塊 | 15 |
冰激凌 | 14 |
蔬菜沙拉 | 9 |
促銷活動:
(1)漢堡套餐5折優惠,每單僅限一套;
(2)全部商品(包括打折套餐)滿20元減4元,滿40元減10元,滿60元減15元,滿80元減20元.
佳佳想要漢堡套餐、雞翅、冰激凌、蔬菜沙拉各一份;點點想要漢堡套餐、雞塊、冰激凌各一份,若他們把想要的都買全,最少要花____________元(含送餐費).
查看答案和解析>>
科目:初中數學 來源: 題型:
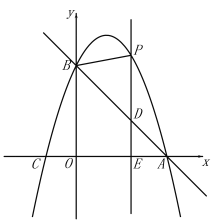
【題目】如圖,直線![]() 與x軸交于點A(3,0),與y軸交于點B,拋物線
與x軸交于點A(3,0),與y軸交于點B,拋物線![]() 經過A,B.
經過A,B.
(1)求拋物線解析式;
(2)E(m,0)是x軸上一動點,過點E作![]() 軸于點E,交直線AB于點D,交拋物線于點P,連接PB.
軸于點E,交直線AB于點D,交拋物線于點P,連接PB.
①點E在線段OA上運動,若△PBD是等腰三角形時,求點E的坐標;
②點E在x軸的正半軸上運動,若![]() ,請直接寫出m的值.
,請直接寫出m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1所示的健身器械為倒蹬機,使用方法為上身不動,腿部向前發力,雙腿伸直之后,然后再慢慢回收.圖2為示意圖,已知![]() 在初始位置,
在初始位置,![]() , 點
, 點![]() 在同一直線上,
在同一直線上,![]() .
.

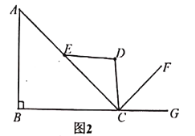
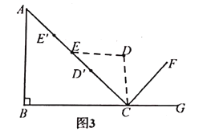
(1)當![]() 在初始位置時,求點
在初始位置時,求點![]() 到
到![]() 的距離;
的距離;
(2)當雙腿伸直后,如圖3,點![]() 分別從初始位置運動到點
分別從初始位置運動到點![]() , 假設
, 假設![]() 三點共線,求此時點
三點共線,求此時點![]() 上升的豎直高度. ( 結果精確到個位) (參考數據:
上升的豎直高度. ( 結果精確到個位) (參考數據:![]()
![]()
![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,一次函數
中,一次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() ,將點
,將點![]() 向右平移2個單位得到點
向右平移2個單位得到點![]() .
.
(1)求點![]() 坐標;
坐標;
(2)如果一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于點
的圖象交于點![]() ,且點
,且點![]() 的橫坐標為1.
的橫坐標為1.
①![]() 時,求
時,求![]() 的值;
的值;
②當![]() 時,直接寫出
時,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩人依次測量同一圓柱體工件的橫截面直徑(單位:![]() ),測得的數據分別如表1、表2.
),測得的數據分別如表1、表2.
表1:甲的測量數據
測量數據 | 9.8 | 9.9 | 10 | 10.1 | 10.3 |
頻數 | 1 | 3 | 3 | 2 | 1 |
表2:乙的測量數據
測量數據 | 9.7 | 9.8 | 10 | 10.1 | 10.3 |
頻數 | 1 | 2 | 3 | 2 | 2 |
(1)如果在這些測量數據中選擇一個數據作為工件直徑的估計值,應該是那個數據?請說明理由.
(2)如果甲再測量一次,求他測量出的數據恰好是估計值的概率;
(3)請直接判斷甲乙兩人誰的測量技術更好______(填甲或乙),你選擇的統計量是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
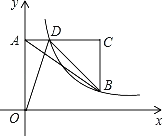
【題目】如圖,在平面直角坐標系中,點A在y軸正半軸上,AC∥x軸,點B、C的橫坐標都是3,且BC=2,點D在AC上,若反比例函數y=![]() (x>0)的圖象經過點B、D.且AO:BC=3:2.
(x>0)的圖象經過點B、D.且AO:BC=3:2.
(1)求點D坐標;
(2)將△AOD沿著OD折疊,設頂點A的對稱點為A′,試判斷點A′是否恰好落在直線BD上,為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數![]() 的圖像與雙曲線
的圖像與雙曲線![]()
![]() 相交于
相交于![]() 和
和![]() 兩點,與
兩點,與![]() 軸相交于點
軸相交于點![]() ,過點
,過點![]() 作
作![]() 軸,垂足為點
軸,垂足為點![]() .
.
(1)求一次函數的解析式;
(2)根據圖像直接寫出不等式![]() 的解集;
的解集;
(3)![]() 的面積為
的面積為
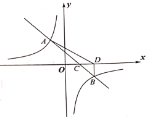
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,以BC為直徑作半圓O,以點D為圓心、DA為半徑做圓弧交半圓O于點P.連結DP并延長交AB于點E.
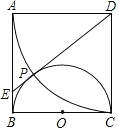
(1)求證:DE為半圓O的切線;
(2)求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com