【題目】如圖，已知二次函數
過（﹣2，4），（﹣4，4）兩點．
（1）求二次函數
的解析式；
（2）將沿x軸翻折，再向右平移2個單位，得到拋物線
，直線y=m（m＞0）交于M、N兩點，求線段MN的長度（用含m的代數式表示）；
（3）在（2）的條件下，、交于A、B兩點，如果直線y=m與、的圖象形成的封閉曲線交于C、D兩點（C在左側），直線y=﹣m與、的圖象形成的封閉曲線交于E、F兩點（E在左側），求證：四邊形CEFD是平行四邊形．
【答案】（1）
；（2）
；（3）證明見解析．
【解析】
試題分析：（1）根據待定系數法即可解決問題．
（2）先求出拋物線y2的頂點坐標，再求出其解析式，利用方程組以及根與系數關系即可求出MN．
（3）用類似（2）的方法，分別求出CD、EF即可解決問題．
試題解析：（1）∵二次函數
過（﹣2，4），（﹣4，4）兩點，∴
，解得：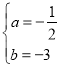
，∴二次函數
的解析式．
（2）∵=
，∴頂點坐標（﹣3，
），∵將沿x軸翻折，再向右平移2個單位，得到拋物線
，∴拋物線的頂點坐標（﹣1，
），∴拋物線為
，由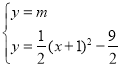
，消去y整理得到
，設
，
是它的兩個根，則MN=
=
=；
（3）由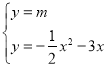
，消去y整理得到
，設兩個根為，，則CD===
，由
，消去y得到
，設兩個根為，，則EF===，∴EF=CD，EF∥CD，∴四邊形CEFD是平行四邊形．
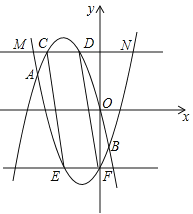
優質課堂快樂成長系列答案科目：初中數學 來源： 題型：
【題目】把下面的推理過程補充完整，并在括號內注明理由．
如圖，點B、D在線段AE上，BC∥EF，AD=BE，BC=EF，
試說明：（1）∠C=∠F；（2）AC∥DF．
解：（1）∵AD=BE（已知）
∴AD+DB=DB+BE（ ① ）
即AB=DE
∵BC∥EF（已知）
∴∠ABC=∠（ ② ） （ ③ ）
又∵BC=EF（已知）
∴△ABC≌△DEF（ ④ ）
∴∠C=∠F，∠A=∠FDE（ ⑤ ）
∴AC∥DF（ ⑥ ）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，半徑均為
個單位長度的半圓
， 
， 
…….組成一條平滑的曲線，點
從原點
出發，沿這條曲線向右運動，速度為每秒
個單位長度,則第
時，點
的坐標是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校組織學生書法比賽，對參賽作品按A、B、C、D四個等級進行了評定．現隨機取部分學生書法作品的評定結果進行分析，并繪制扇形統計圖和條形統計圖如下：
根據上述信息完成下列問題：
（1）求這次抽取的樣本的容量；
（2）請在圖②中把條形統計圖補充完整；
（3）已知該校這次活動共收到參賽作品750份，請你估計參賽作品達到B級以上（即A級和B級）有多少份？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com