
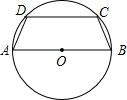
 如圖,⊙O是圓木截面,四邊形ABCD是從這個圓木鋸下的木版橫截面,其中AB為直徑,AD=BC
如圖,⊙O是圓木截面,四邊形ABCD是從這個圓木鋸下的木版橫截面,其中AB為直徑,AD=BC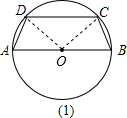 (1)解:連接OD、OC,由∠BAD=75°,OA=OD知∠AOD=30°,
(1)解:連接OD、OC,由∠BAD=75°,OA=OD知∠AOD=30°, 的長為5πcm.
的長為5πcm.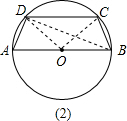
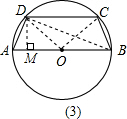
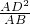 =
= ,
,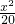 ,
,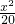 +40=-
+40=- x2+2x+80=-
x2+2x+80=- (x-20)2+100,
(x-20)2+100,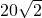 ,
,

 天天向上口算本系列答案
天天向上口算本系列答案科目:初中數學 來源: 題型:
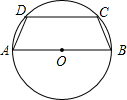 如圖,⊙O是圓木截面,四邊形ABCD是從這個圓木鋸下的木版橫截面,其中AB為直徑,AD=BC
如圖,⊙O是圓木截面,四邊形ABCD是從這個圓木鋸下的木版橫截面,其中AB為直徑,AD=BC查看答案和解析>>
科目:初中數學 來源:2009年江蘇省連云港市中考數學原創試卷大賽(42)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com