【題目】如圖是二次函數y=（x+m）2+k的圖象，其頂點坐標為M（1，﹣4）
（1）求出圖象與x軸的交點A、B的坐標；
（2）在二次函數的圖象上是否存在點P，使S△PAB=
S△MAB？若存在，求出點P的坐標；若不存在，請說明理由．
【答案】（1）A（﹣1，0），B（3，0）;（2）存在合適的點P，坐標為（4，5）或（﹣2，5）．
【解析】試題分析：
（1）由二次函數y=（x+m）2+k的頂點坐標為M（1，﹣4）可得解析式為： 
，解方程： 
可得點A、B的坐標；
（2）設點P的縱坐標為
，由△PAB與△MAB同底，且S△PAB=
S△MAB，可得： 
，從而可得
=
，結合點P在拋物線
的圖象上，可得
=5，由此得到： 
，解方程即可得到點P的坐標.
試題解析：
（1）∵拋物線解析式為y=（x+m）2+k的頂點為M（1，﹣4）
∴
，
當y=0時，（x﹣1）2﹣4=0，解得x1=3，x2=﹣1，
∴A（﹣1，0），B（3，0）；
（2）∵△PAB與△MAB同底，且S△PAB=
S△MAB，
∴
，即
=
，
又∵點P在y=（x﹣1）2﹣4的圖象上，
∴yP≥﹣4，
∴
=5，則
，解得： 
，
∴存在合適的點P，坐標為（4，5）或（﹣2，5）．
科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系中，將含
的三角尺的直角頂點
落在第二象限，其斜邊兩端點
、
分別落在
軸、
軸上，且
．
（
）若
．
①求點
的坐標．
②若點
向右滑動
，求點
向上滑動的距離．
（
）點
、
分別在
軸、
軸上滑動，則點
于點
的距離的最大值
__________ 
．（直接寫出答案）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場在某一時間以每件60元的價格賣出兩件衣服，其中一件盈利25%，另一件虧損25%，賣這兩件衣服總的是（ ）
A.盈利8元B.虧損8元C.不盈不虧D.虧損15元
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在如圖所示的方格圖中，我們稱每個小正方形的頂點為“格點”，以格點為頂點的三角形叫做“格點三角形”，根據圖形，回答下列問題.
（1）圖中格點三角形A′B′C′是由格點三角形ABC通過怎樣的平移得到的？
（2）如果以直線a，b為坐標軸建立平面直角坐標系后，點A的坐標為(－3，4)，請寫出格點三角形DEF各頂點的坐標，并求出三角形DEF的面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
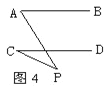
【題目】①如圖1,AB∥CD,則∠A +∠E +∠C=180°；②如圖2,AB∥CD,則∠E =∠A +∠C;③如圖3,AB∥CD,則∠A +∠E－∠1=180° ； ④如圖4,AB∥CD,則∠A=∠C +∠P.以上結論正確的個數是( )
A. 、1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于平面直角坐標系xOy中的點P（a，b），若點P′的坐標為（a＋kb，ka＋b）（其中k為常數，且k≠0），則稱點P′為點P的“k屬派生點”．
例如：P（1，4）的“2屬派生點”為P′（1＋2×4，2×1＋4），即P′（9，6）．
（1）點P（－1，6）的“2屬派生點”P′的坐標為_____________；
（2）若點P的“3屬派生點”P′的坐標為（6，2），則點P的坐標___________；
（3）若點P在x軸的正半軸上，點P的“k屬派生點”為P′點，且線段PP′的長度為線段OP長度的2倍，求k的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com