Question

如圖,矩形紙片ABCD中,AB=8,將紙片折疊,使頂點B落在邊AD的E點上,BG=10.

(1)當折痕的另一端F在AB邊上時,如圖(1).求△EFG的面積.

(2)當折痕的另一端F在AD邊上時,如圖(2).證明四邊形BGEF為菱形,并求出折痕GF的長. 

 

 

Answer 1

【答案】

解:(1)過點G作GH⊥AD,

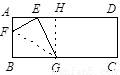
則四邊形ABGH為矩形,

∴GH=AB=8,AH=BG=10,

由圖形的折疊可知△BFG≌△EFG,

∴EG=BG=10,∠FEG=∠B=90°；∴EH=6,AE=4,∠AEF+∠HEG=90°,

∵∠AEF+∠AFE=90°,

∴∠HEG=∠AFE,

又∵∠EHG=∠A=90°,

∴△EAF∽△EHG,

∴,∴EF=5,

∴S_△EFG=EF·EG=×5×10=25.

(2)由圖形的折疊可知四邊形ABGF≌四邊形HEGF,

∴BG=EG,AB=EH,∠BGF=∠EGF,

∵EF∥BG，∴∠BGF=∠EFG,∴∠EGF =∠EFG,∴EF=EG,

∴BG=EF,∴四邊形BGEF為平行四邊形,

又∵EF=EG,∴平行四邊形BGEF為菱形；

連結BE，BE、FG互相垂直平分，

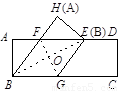
在Rt△EFH中,EF=BG=10,EH=AB=8,

由勾股定理可得FH=AF=6，∴AE=16，

∴BE==8，∴BO=4，

∴FG=2OG=2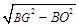=4。

【解析】根據軸對稱的性質，折疊前后圖形的形狀和大小不變和矩形的性質及直角三角形的性質，同角的余角相等，相似三角形的判定和性質，平行四邊形和菱形的判定和性質求解．