


|


科目:初中數學 來源: 題型:


查看答案和解析>>
科目:初中數學 來源: 題型:
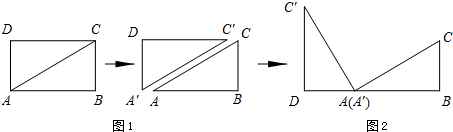
1.情境觀察 將矩形ABCD紙片沿對角線AC剪開,得到△ABC和△A′C′D,如圖1所示.將△A′C′D的頂點A′與點A重合,并繞點A按逆時針方向旋轉,使點D、A(A′)、B在同一條直線上,如圖2所示.觀察圖2可知:與BC相等的線段是 ,∠CAC′= °.

2.問題探究 如圖3,△ABC中,AG⊥BC于點G,以A為直角頂點,分別以AB、AC為直角邊,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,過點E、F作射線GA的垂線,垂足分別為P、Q. 試探究EP與FQ之間的數量關系,并證明你的結論.

3.拓展延伸 如圖4,△ABC中,AG⊥BC于點G,分別以AB、AC為一邊向△ABC外作矩形ABME和矩形ACNF,射線GA交EF于點H. 若AB= k AE,AC= k AF,試探究HE與HF之間的數量關系,并說明理由

查看答案和解析>>
科目:初中數學 來源:2012屆浙江省椒江區九年級二模數學試卷(帶解析) 題型:解答題
【小題1】情境觀察 將矩形ABCD紙片沿對角線AC剪開,得到△ABC和△A′C′D,如圖1所示.將△A′C′D的頂點A′與點A重合,并繞點A按逆時針方向旋轉,使點D、A(A′)、B在同一條直線上,如圖2所示.觀察圖2可知:與BC相等的線段是 ,∠CAC′= °.
【小題2】問題探究 如圖3,△ABC中,AG⊥BC于點G,以A為直角頂點,分別以AB、AC為直角邊,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,過點E、F作射線GA的垂線,垂足分別為P、Q. 試探究EP與FQ之間的數量關系,并證明你的結論.
【小題3】拓展延伸 如圖4,△ABC中,AG⊥BC于點G,分別以AB、AC為一邊向△ABC外作矩形ABME和矩形ACNF,射線GA交EF于點H. 若AB=" k" AE,AC=" k" AF,試探究HE與HF之間的數量關系,并說明理由
查看答案和解析>>
科目:初中數學 來源:2012屆湖南省九年級下學期第一次月考考試數學卷 題型:選擇題
(本題滿分10分)
情境觀察
將矩形ABCD紙片沿對角線AC剪開,得到△ABC和△A′C′D,如圖1所示.將△A′C′D的頂點A′與點A重合,并繞點A按逆時針方向旋轉,使點D、A(A′)、B在同一條直線上,如圖2所示.觀察圖2可知:與BC相等的線段是 ▲ ,∠CAC′= ▲ °.
 |
 問題探究
問題探究
如圖3,△ABC中,AG⊥BC于點G,以A為直角頂點,分
別以AB、AC為直角邊,向△ABC外作等腰Rt△ABE和等
腰Rt△ACF,過點E、F作射線GA的垂線,垂足分別為
P、Q. 試探究EP與FQ之間的數量關系,并證明你的結論.
拓展延伸
如圖4,△ABC中,AG⊥BC于點G,分別以AB、AC為一邊向△ABC外作矩形ABME和矩形ACNF,射線GA交EF于點H. 若AB= k AE,AC= k AF,試探究HE與HF之間的數量關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com