【答案】
分析:先整理式子
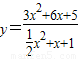
得(y-6)x
2+(2y-12)x+2y-10=0,此時△≥0,得出y的范圍由此即可求得y的最小值.
解答:解:將函數
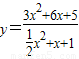
整理為關于x的一元二次方程得:
(y-6)x
2+(2y-12)x+2y-10=0,(y-6≠0),
由x為實數,
∴△=(2y-12)
2-4(y-6)(2y-10)≥0,
化簡得出不等式y
2-10y+24≤0,
解得4≤y≤6(y≠6),
當y取最小值4時,x=-1,
∴分式的最小值為4.
故答案為:4.
點評:本題考查了二次函數的最值,難度一般,此類題關鍵是把原函數式整理化簡為關于x的一元二次方程.

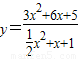 的最小值是 .
的最小值是 .