Question

（1）如圖1，若⊙O₁與⊙O₂外切于A，BC是⊙O₁與⊙O₂外公切線，B、C為切點，求證：AB⊥AC．
（2）如圖2，若⊙O₁與⊙O₂外離，BC是⊙O₁與⊙O₂的外公切線，B、C為切點，連心線O₁O₂分別交⊙O₁、⊙O₂于M、N，BM、CN的延長線交于P，則BP與CP是否垂直？證明你的結論．
（3）如圖3，若⊙O₁與⊙O₂相交，BC是⊙O₁與⊙O₂的公切線，B、C為切點，連心線O₁O₂分別交⊙O₁、⊙O₂于M、N，Q是線段MN上一點，連接BQ、CQ，則BQ與CQ是否垂直？證明你的結論．

Answer 1

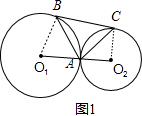
（1）證明：如圖1，連接O₁A，O₂C，
∵BC是兩圓的外公切線，
∴∠O₁BC=∠O₂CB=90°，
∴O₁B∥O₂C，
∴∠O₁+∠O₂=180°，
∵∠O₁AB=∠O₁BA=（180°-∠O₁）=90°-∠O₁=90°-∠ABC，
∴∠ABC=∠O₁，
同理：∠ACB=∠O₂，
∴∠ABC+∠ACB=（∠O₁+∠O₂）=90°，
∴∠BAC=90°．
∴AB⊥AC；

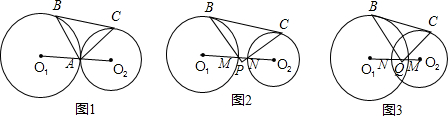
（2）解：BP⊥CP．
證明：如圖2，連接O₁B，O₂C，
∵BC是兩圓的外公切線，
∴∠O₁BC=∠O₂CB=90°，
∴O₁B∥O₂C，
∴∠O₁+∠O₂=180°．
∠O₁BM=∠O₁MB=（180°-∠O₁）=90°-∠O₁=90°-∠PBC，
∴∠PBC=∠O₁，
同理：∠PCB=∠O₂，
∴∠PBC+∠PCB=（∠O₁+∠O₂）=90°，
∴∠BPC=90°，
∴BP⊥CP；

（3）解：BQ與CQ不垂直．
證明：如圖3，連接O₁B，O₂C，
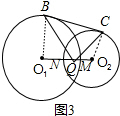
∵BC是兩圓的外公切線，
∴∠O₁BC=∠O₂CB=90°，
∴O₁B∥O₂C，
∴∠O₁+∠O₂=180°．
∵O₁B＞O₁Q，
∴∠O₁QB＞∠O₁BQ，
同理：∠O₂QC＞∠O₂CQ，
∴∠O₁QB+∠O₂QC＞∠O₁BQ+∠O₂CQ，
∴∠O₁QB+∠O₂QC＞90°，
∴∠BQC＜90°
∴BQ與CQ不垂直．
分析：（1）連接O₁B，O₂C，根據切線的性質可以得到∠O₁BC=∠O₂CB=90°，再用△O₁AB，△O₂AC的內角和是180°進行證明．
（2）連接O₁B，O₂C，根據切線的性質得到∠O₁BC=∠O₂CB=90°，再用三角形的內角和以及對頂角的性質進行證明．
（3）連接O₁B，O₂C，根據切線的性質得到∠O₁BC=∠O₂CB=90°，然后用三角形中大邊對大角以及三角形的內角和定理進行證明．
點評：本題考查圓與圓的位置關系，（1）中兩圓是外切的，AB是兩圓的公切線，根據切線的性質和三角形內角和定理進行證明．（2）中兩圓是外離的，仍然可以用切線的性質和三角形的內角和定理進行證明．（3）中兩圓是相交的，先用切線的性質得到90°的角，然后在三角形中用大邊對大角以及三角形的內角和證明兩直線不垂直．