
【題目】某化妝品專賣店,為了吸引顧客,準備在“母親節”當天舉辦了甲、乙兩種品牌化妝品有獎酬賓活動,凡購物滿![]() 元,均可得到一次搖獎的機會.已知在搖獎機內裝有
元,均可得到一次搖獎的機會.已知在搖獎機內裝有![]() 個紅球和
個紅球和![]() 個白球,除顏色外其它都相同,搖獎者必須從搖獎機中一次連續搖出兩個球,根據球的顏色決定送禮金券的多少(如下表):
個白球,除顏色外其它都相同,搖獎者必須從搖獎機中一次連續搖出兩個球,根據球的顏色決定送禮金券的多少(如下表):

(![]() )請你用列表法(或畫樹狀圖法)求一次連續搖出一紅一白兩球的概率;
)請你用列表法(或畫樹狀圖法)求一次連續搖出一紅一白兩球的概率;
(![]() )如果一個顧客當天在本店購物滿
)如果一個顧客當天在本店購物滿![]() 元,若只考慮獲得最多的禮品卷,請你幫助分析選擇購買哪種品牌的化妝品?并說明理由.
元,若只考慮獲得最多的禮品卷,請你幫助分析選擇購買哪種品牌的化妝品?并說明理由.
【答案】(![]() )樹狀圖見解析,
)樹狀圖見解析, ![]() ;(
;(![]() )甲,理由見解析.
)甲,理由見解析.
【解析】試題分析:(1)搖獎機內有兩紅兩白球,標記為紅1,紅2,白1,白2,連續搖出一紅一白,先出來的球有四種情況,且概率相等,分別為紅1,紅2,白1,白2,畫出樹狀圖,再寫出后出來球的情況,如上圖所示進而找出一紅一白的結果有8種,占所有可能出現的結果12種的三分之二.
(2)先在(1)的基礎上再算出另外兩種情況出現的概率,根據算出的概率,依據甲乙化妝品獲得禮品券的方案分別算出獲得禮品券,取獲得禮品券多的品牌化妝品.
試題解析:(1)用樹狀圖列出所有可能的結果:
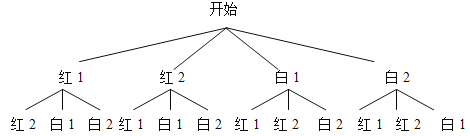
由樹狀圖可知,所有可能出現的結果共有12種,且每種結果出現的可能性相同,其中恰好連續搖出一紅一白的結果有8種,所以P(一紅一白)=![]() .∴一次連續搖出一紅一白兩球的概率為
.∴一次連續搖出一紅一白兩球的概率為![]() .
.
(2)若顧客在本店購物滿88元,由(1)得:P(兩紅)=![]() , P(兩白)=
, P(兩白)=![]() .
.
(3)若購買甲品牌化妝品,則獲得禮品卷為6×![]() +12×
+12×![]() +6×
+6×![]() =10(元);若購買乙品牌化妝品,則獲得禮品卷為12×
=10(元);若購買乙品牌化妝品,則獲得禮品卷為12×![]() +6×
+6×![]() +12×
+12×![]() =8(元).∵10>8,∴顧客應選擇購買甲品牌的化妝品.
=8(元).∵10>8,∴顧客應選擇購買甲品牌的化妝品.


科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線AC、BD相交于點O,CE∥BD,DE∥AC,若AC=4,則四邊形OCED的周長為( )
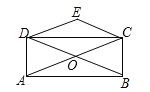
A.4B.8C.10D.12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】ABCD中,E是CD邊上一點,
(1)將△ADE繞點A按順時針方向旋轉,使AD、AB重合,得到△ABF,如圖1所示.觀察可知:與DE相等的線段是 ,∠AFB=∠
(2)如圖2,正方形ABCD中,P、Q分別是BC、CD邊上的點,且∠PAQ=45°,試通過旋轉的方式說明:DQ+BP=PQ;
(3)在(2)題中,連接BD分別交AP、AQ于M、N,你還能用旋轉的思想說明BM2+DN2=MN2嗎?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】AC是□ABCD的一條對角線,過AC中點O的直線分別交AD、BC 于點E、F.

(1)求證:AE=CF;
(2)連接AF,CE.
①當EF⊥AC時,四邊形AFCE是什么四邊形?請證明你的結論;
②若AB=1,BC=2,∠B=60°,則四邊形AFCE為矩形時,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點B,C分別是∠MAN的邊AM、AN上的點,滿足AB=BC,點P為射線的AB上的動點,點D為點B關于直線AC的對稱點,連接PD交AC于E點,交BC于點F。
(1)在圖1中補全圖形;
(2)求證:∠ABE=∠EFC;
(3)當點P運動到滿足PD⊥BE的位置時,在射線AC上取點Q,使得AE=EQ,此時![]() 是否是一個定值,若是請直接寫出該定值,若不是,請說明理由.
是否是一個定值,若是請直接寫出該定值,若不是,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
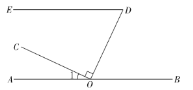
【題目】如圖,點O在直線AB上,OC⊥OD,∠EDO與∠1互余.
(1)求證:ED//AB;
(2)OF平分∠COD交DE于點F,若∠OFD=65°,補全圖形,并求∠1的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C是⊙O上一點,過點C的直線交AB的延長線于點D,AE⊥DC,垂足為E,F是AE與⊙O的交點,AC平分∠BAE,連接OC.
(1)求證:DE是⊙O的切線;
(2)若⊙O半徑為4,∠D=30°,求圖中陰影部分的面積(結果用含π和根號的式子表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀以下材料,并按要求完成相應的任務.
在初中數學課本中重點介紹了提公因式法和運用公式法兩種因式
分解的方法,其中運用公式法即運用平方差公式:![]() 和完全平方公式:
和完全平方公式:![]() 進行分解因式,能運用完全平方公式分解因式的多項式必須是三項式,其中有兩項能寫成兩個數(或式)的平方和的形式,另一項是這兩個數(或式)的積的2倍.當一個二次三項式不能直接能運用完全平方公式分解因式時,可應用下面方法分解因式,先將多項式
進行分解因式,能運用完全平方公式分解因式的多項式必須是三項式,其中有兩項能寫成兩個數(或式)的平方和的形式,另一項是這兩個數(或式)的積的2倍.當一個二次三項式不能直接能運用完全平方公式分解因式時,可應用下面方法分解因式,先將多項式![]()
![]() 變形為
變形為![]() 的形式,我們把這樣的變形方法叫做多項式
的形式,我們把這樣的變形方法叫做多項式![]() 的配方法.再運用多項式的配方法及平方差公式能對一些多項式進行分解因式.
的配方法.再運用多項式的配方法及平方差公式能對一些多項式進行分解因式.
例如:![]()
![]()

![]()
![]() .
.
根據以上材料,完成相應的任務:
(1)利用“多項式的配方法”將![]() 化成
化成![]() 的形式為_______;
的形式為_______;
(2)請你利用上述方法因式分解:
①![]() ; ②
; ②![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com