
 .
. ﹣m(0<m<
﹣m(0<m< )時,請直接寫出到△ABD的三邊所在直線的距離相等的所有點的坐標(用含m的式子表示).
)時,請直接寫出到△ABD的三邊所在直線的距離相等的所有點的坐標(用含m的式子表示).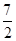 x+2.②
x+2.②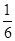 .(2)P1(
.(2)P1( ﹣m,1),P2(
﹣m,1),P2( ﹣m,﹣3),P3(﹣
﹣m,﹣3),P3(﹣ ﹣m,3),P4(3
﹣m,3),P4(3 ﹣m,3).
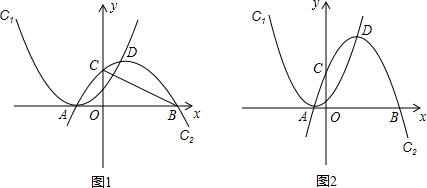
﹣m,3). 時,拋物線C1:y=(x+
時,拋物線C1:y=(x+ )2.
)2. )2).
)2). )2(I).
)2(I). )2=2,
)2=2,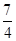 ,代入(I)式,
,代入(I)式,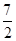 x+2.
x+2. )2=0,解得x=2a+
)2=0,解得x=2a+ 或x=﹣
或x=﹣ ,∴B(2a+,0);
,∴B(2a+,0);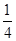 ,∴C(0,a+
,∴C(0,a+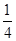 ).
).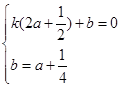 ,解得
,解得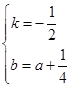 ,
, x+(a+
x+(a+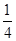 ).
).
 a+
a+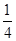 ),PE=
),PE= a+
a+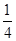 .
.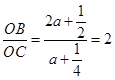 ,
,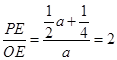 ,
,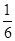 .
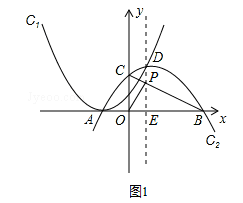
. ,使得線段BC上有一點P,滿足點B與點C到直線OP的距離之和最大且AP="BP"
,使得線段BC上有一點P,滿足點B與點C到直線OP的距離之和最大且AP="BP"  ﹣m,
﹣m, ﹣m,
﹣m, ﹣m.
﹣m. ﹣m,3).
﹣m,3). ﹣m+m=2
﹣m+m=2 .
. ,OE=OB﹣BE=
,OE=OB﹣BE= ﹣m.
﹣m.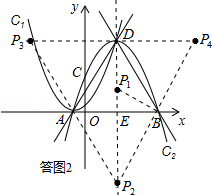
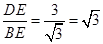 ,
, ×
×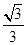 =1,
=1, ﹣m,1);
﹣m,1); •
• =3,
=3, ﹣m,﹣3);
﹣m,﹣3); ,且P3P4∥x軸.
,且P3P4∥x軸. ﹣m,3)、P4(3
﹣m,3)、P4(3 ﹣m,3).
﹣m,3). ﹣m,1),P2(
﹣m,1),P2( ﹣m,﹣3),P3(﹣
﹣m,﹣3),P3(﹣ ﹣m,3),P4(3
﹣m,3),P4(3 ﹣m,3).
﹣m,3).

 星級口算天天練系列答案
星級口算天天練系列答案科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
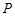 的橫坐標,將它所對的面的數字作為點
的橫坐標,將它所對的面的數字作為點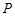 的縱坐標,則點
的縱坐標,則點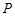 落在拋物線
落在拋物線 與
與 軸所圍成的區域內(不含邊界)的概率是 .
軸所圍成的區域內(不含邊界)的概率是 .查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
| 1 |
| 2 |

查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題

| A.c>0 | B.2a+b=0 | C.b2﹣4ac>0 | D.a﹣b+c>0 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
 ,BC=6,點E為對角線AC的中點,點P在邊BC上,連接PE、PA.當點P在BC上運動時,設BP=x,△APE的周長為y,下列圖象中,能表示y與x的函數關系的圖象大致是( )
,BC=6,點E為對角線AC的中點,點P在邊BC上,連接PE、PA.當點P在BC上運動時,設BP=x,△APE的周長為y,下列圖象中,能表示y與x的函數關系的圖象大致是( )
 B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com