
【題目】商場經銷甲、乙兩種商品,甲種商品每件進價15元,售價20元;乙種商品每件進價35元,售價45元.
(1)若該商場同時購進甲、乙兩種商品共100件恰好用去2700元,求能購進甲、乙兩種商品各多少件?
(2)該商場為使甲、乙兩種商品共100件的總利潤(利潤=售價![]() 進價)不少于750元,且不超過760元,請你幫助該商場設計相應的進貨方案.
進價)不少于750元,且不超過760元,請你幫助該商場設計相應的進貨方案.
【答案】(1)甲種商品40件,乙種商品60件.
(2)方案一:購進甲種商品48件,乙種商品52件;方案二:購進甲種商品49件,乙種商品51件;方案三:購進甲種商品50件,乙種商品50件.
【解析】
試題分析:(1)等量關系為:甲商品總進價+乙商品總進價=2700,根據此關系列方程即可求解;
(2)關系式為:甲商品件數×(20-15)+乙商品件數×(45-35)≥750,甲商品件數×(20-15)+乙商品件數×(45-35)≤760;
(3)第一天的總價為200元,打折最低應該出270元,所以沒有享受打折,第二天的也可能享受了9折,也可能享受了8折.應先算出原價,然后除以單價,得出數量.
試題解析:(1)設購進甲、乙兩種商品分別為x件,(100-x)件,根據題意得:
15x+35(100-x)=2700,
解得x=40,
則100-40=60(件),
答:甲種商品40件,乙種商品60件.
(2)設該商場進甲種商品a件,則購進乙種商品(100-a)件,根據題意得
(20-15)a+(45-35)(100-a)≥750,
(20-15)a+(45-35)(100-a)≤760,
因此,不等式組的解集為48≤a≤50.
根據題意得值應是整數,所以a=48或a=49或a=50,
該商場共有三種進貨方案:
方案一:購進甲種商品48件,乙種商品52件;
方案二:購進甲種商品49件,乙種商品51件;
方案三:購進甲種商品50件,乙種商品50件.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】2004年6月3日中央新聞報道,為鼓勵居民節約用水,北京市將出臺新的居民用水收費標準:①若每月每戶居民用水不超過4立方米,則按每立方米2元計算;②若每月每戶居民用水超過4立方米,則超過部分按每立方米4.5元計算(不超過部分仍按每立方米2元計算).現假設該市某戶居民某月用水x立方米,水費為y元,則y與x的函數關系用圖象表示正確的是( )
A.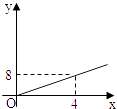
B.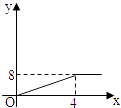
C.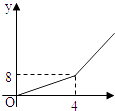
D.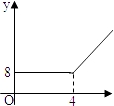
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠計劃生產A、B兩種產品共50件,需購買甲、乙兩種材料.生產一件A產品需甲種材料30千克、乙種材料10千克;生產一件B產品需甲、乙兩種材料各20千克.經測算,購買甲、乙兩種材料各1千克共需資金40元,購買甲種材料2千克和乙種材料3千克共需資金105元.
(1)甲乙兩種材料每千克分別是多少元?
(2)現工廠用于購買甲、乙兩種材料的資金不超過38000元,且生產B產品不少于28件,問符合條件的生產方案有哪幾種?
(3)在(2)的條件下,若生產一件A產品需加工費200元,生產一件B產品需加工費300元,應選擇哪種生產方案,使生產這50件產品的成本最低?(成本=材料費+加工費)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com