
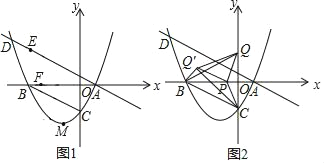
【題目】如圖1,在平面直角坐標系中,拋物線y=![]() 與x軸交于A,B兩點,交y軸于點C,連接BC.過點A作BC的平行線交拋物線于點D.
與x軸交于A,B兩點,交y軸于點C,連接BC.過點A作BC的平行線交拋物線于點D.
(1)求△ABC的面積;
(2)已知點M是拋物線的頂點,在直線AD上有一動點E,x軸上有一動點F,當ME+BE最小時,求|CF﹣EF|的最大值及此時點F的坐標;
(3)如圖2,在y軸正半軸上取點Q,使得CB=CQ,點P是x軸上一動點,連接PC,將△CPQ沿PC折疊至△CPQ′.連接BQ,BQ′,QQ′,當△BQQ′為等腰三角形時,直接寫出點P的坐標.
【答案】(1)S△ABC=6![]() ;(2)|CF﹣EF|的最大值為2,點F的坐標為(﹣3
;(2)|CF﹣EF|的最大值為2,點F的坐標為(﹣3![]() ,0);(3)點P的坐標為(3
,0);(3)點P的坐標為(3![]() ﹣6,0),(﹣3
﹣6,0),(﹣3![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)分別將x=0和y=0代入解析式即可求出A,B,C三點的坐標,即可求出△ABC的面積;
(2)先證△ABC是直角三角形,再作點B關于直線AD的對稱點B',連接MB',交AD于E,則此時ME+BE有最小值,作點E關于x軸的對稱點E',連接CE'并延長CE'交x軸于F,則此時|CF﹣EF|有最大值,為CE'的長度,根據點的坐標求出CE'的長度,此時點F與點B重合,即知點F坐標;
(3)分三種情況通過等邊三角形,直角三角形的性質及勾股定理求出點P的坐標.
解:(1)在拋物線y=![]() 中,
中,
當y=0時,x1=﹣3![]() ,x2=
,x2=![]() ,
,
∴A(![]() ,0),B(﹣3
,0),B(﹣3![]() ,0),
,0),
當x=0時,y=﹣3,
∴C(0,﹣3),
連接AC,
∴S△ABC=![]() ABOC=6
ABOC=6![]() ;
;
(2)在Rt△ABC中,
AC=![]() =2
=2![]() ,
,
BC=![]() =6,
=6,
AB=4![]() ,
,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
∴tan∠ABC=![]() ,
,
∴∠ABC=30°,
如圖,作點B關于直線AD的對稱點B',連接MB',交AD于E,則此時ME+BE有最小值,
且∠CBB'=90°,∠ABB'=60°,
連接AB',則AB=AB',
∴△ABB'為等邊三角形,
∴BB'=AB',
∴點B'在AB的垂直平分線上,
又∵M為拋物線頂點,
∴點M,B'同為拋物線對稱軸上的點,
∵拋物線對稱軸為x=![]() =﹣
=﹣![]() ,
,
∴xE=﹣![]() ,
,
將C(0,﹣3),B(﹣3![]() ,0)代入一次函數解析式,
,0)代入一次函數解析式,
得![]() ,
,
解得k=﹣![]() ,b=﹣3,
,b=﹣3,
∴yBC=﹣![]() x﹣3,
x﹣3,
∵BC∥AD,
∴設yAD=﹣![]() x+b,
x+b,
將A(![]() ,0)代入,
,0)代入,
得b=﹣1,
∴yAD=﹣![]() x﹣1,
x﹣1,
當xE=﹣![]() 時,yE=2,
時,yE=2,
∴E(﹣![]() ,2),
,2),
作點E關于x軸的對稱點E'(﹣![]() ,﹣2),
,﹣2),
連接CE'并延長CE'交x軸于F,則此時|CF﹣EF|有最大值,為CE'的長度,
CE'=![]() =2,
=2,
理由如下:
在x軸上F外任取一點F',連接F'E',CF',
在△CE'F'中,都有|CF'﹣EE'|<CE',
∴當CE'F在一條直線上時,|CF﹣EF|有最大值,
將C(0,﹣3)E'(﹣![]() ,﹣2)代入一次函數解析式,
,﹣2)代入一次函數解析式,
得![]() ,
,
解得k=﹣![]() ,b=﹣3,
,b=﹣3,
∴yCE'=﹣![]() x﹣3,
x﹣3,
∴直線CE'與直線CB重合,
∴點F與點B重合,
∴點F的坐標為(﹣3![]() ,0),
,0),
∴|CF﹣EF|的最大值為2
CE'=![]() =2;此時點F的坐標為(﹣3
=2;此時點F的坐標為(﹣3![]() ,0);
,0);
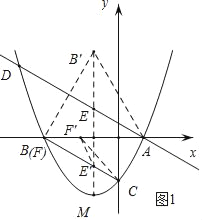
(3)①如圖2﹣1,當Q'B=Q'Q時,
由(1)知∠ABC=30°,
∴∠BCA=60°,
∵CB=CQ,
∴△CBQ為等邊三角形,
∴CQ=BC=6,
又∵BQ'=QQ',
∴∠BCQ'=∠QCQ’=30°,∠CBQ'=∠CQ'B=∠CQ'Q=∠CQQ'=75°,
∴∠Q'CP=∠QCP=∠PQ'C=∠PQC=15°,
∴∠Q'PQ=60°,
∴△QQ'P是等邊三角形,△BQ'P是等腰直角三角形,
設PQ=a,
則QQ'=Q'P=Q'B=a,
∴BP=![]() a,
a,
在Rt△QPO中,QP2=OP2=OQ2,
∴a2+(3![]() ﹣
﹣![]() a)2+32,
a)2+32,
解得a1=3![]() +3
+3![]() (舍去),a2=3
(舍去),a2=3![]() ﹣3
﹣3![]() ,
,
∴BP=![]() a=6
a=6![]() ﹣6,
﹣6,
∴OP=6﹣3![]() ,
,
∴P(3![]() ﹣6,0);
﹣6,0);

②如圖2﹣2,當BQ=BQ'時,點P與點B重合,
∴P(﹣3![]() ,0);
,0);
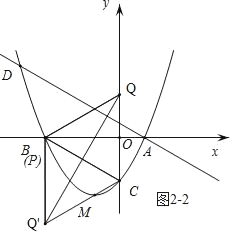
③如圖2﹣3,當QB=QQ'時,點P與點A重合,
∴P(﹣![]() ,0).
,0).

綜上所述,當△BQQ′為等腰三角形時,點P的坐標為(3![]() ﹣6,0),(﹣3
﹣6,0),(﹣3![]() ,0)或(
,0)或(![]() ,0).
,0).


科目:初中數學 來源: 題型:
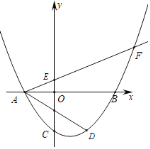
【題目】如圖,在平面直角坐標系xOy中,已知拋物線![]() 與x軸交于點A、
與x軸交于點A、![]() 在B左側
在B左側![]() ,與y軸交于點C,經過點A的射線AF與y軸正半軸相交于點E,與拋物線的另一個交點為F,
,與y軸交于點C,經過點A的射線AF與y軸正半軸相交于點E,與拋物線的另一個交點為F,![]() ,點D是點C關于拋物線對稱軸的對稱點,點P是y軸上一點,且
,點D是點C關于拋物線對稱軸的對稱點,點P是y軸上一點,且![]() ,則點P的坐標是______.
,則點P的坐標是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E,F是平行四邊形ABCD對角線AC上兩點,AE=CF=![]() AC.連接DE,DF并延長,分別交AB,BC于點G,H,連接GH,則
AC.連接DE,DF并延長,分別交AB,BC于點G,H,連接GH,則![]() 的值為( )
的值為( )
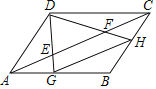
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,矩形ABCD中,E是AD的中點,以點E直角頂點的直角三角形EFG的兩邊EF,EG分別過點B,C,∠F=30°.
(1)求證:BE=CE
(2)將△EFG繞點E按順時針方向旋轉,當旋轉到EF與AD重合時停止轉動.若EF,EG分別與AB,BC相交于點M,N.(如圖2)
①求證:△BEM≌△CEN;
②若AB=2,求△BMN面積的最大值;
③當旋轉停止時,點B恰好在FG上(如圖3),求sin∠EBG的值.



查看答案和解析>>
科目:初中數學 來源: 題型:
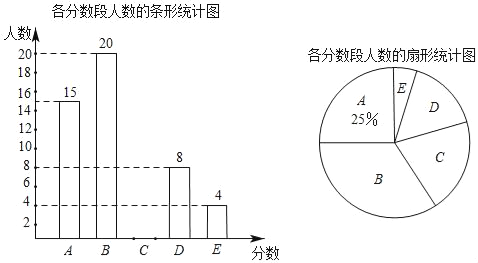
【題目】今年9月28日,某中學初三年級同學進行了中招體育模擬考試,王老師為了更加科學有效地制定后期訓練計劃,對本班同學的體考成績進行了統計,并繪制了如圖的條形統計圖和扇形統計圖,其中體育成績共分為五個等級:A:46分﹣50分;B:41分﹣45分C:36分﹣40分;D:31分﹣35分;E:30分及以下,請根據圖中所給的信息完成下列問題:
(1)將上面的條形統計圖補充完整:并計算扇形統計圖中E等級所對應的圓心角度數為 .
(2)該班A等級中共有5名同學獲得滿分,其中男同學只有2名,現從這5名同學中任選2名同學在班上進行經驗交流,請用樹狀圖或列表法求恰好選到一名男同學和一名女同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c(a≠0)的圖象與x軸的相交情況,關于下列結論:
①方程ax2+bx=0的兩個根為x1=0,x2=﹣4;②b﹣4a=0;③9a+3b+c<0;其中正確的結論有( )
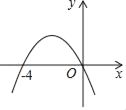
A. 0個B. 1個C. 2個D. 3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖拋物線y=ax2+bx+c的對稱軸為直線x=1,且過點(3,0),下列結論:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正確的有( )個.
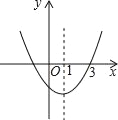
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,對于點P(x,y),若點Q的坐標為(x,|x﹣y|),則稱點Q為點P的“關聯點”.
(1)請直接寫出點(2,2)的“關聯點”的坐標;
(2)如果點P在函數y=x﹣1的圖象上,其“關聯點”Q與點P重合,求點P的坐標;
(3)如果點M(m,n)的“關聯點”N在函數y=x2的圖象上,當0≤m≤2時,求線段MN的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
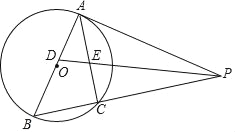
【題目】如圖,以AB為直徑的⊙O外接于△ABC,過A點的切線AP與BC的延長線交于點P,∠APB的平分線分別交AB,AC于點D,E,其中AE,BD(AE<BD)的長是一元二次方程x2﹣5x+6=0的兩個實數根.
(1)求證:PABD=PBAE;
(2)在線段BC上是否存在一點M,使得四邊形ADME是菱形?若存在,請給予證明,并求其面積;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com