
【題目】為執行“均衡教育”政策,我縣2015年投入教育經費2500萬元,預計2017年投入3600萬元,若每年投入教育經費的年平均增長百分率為x,則可列方程為 .
科目:初中數學 來源: 題型:
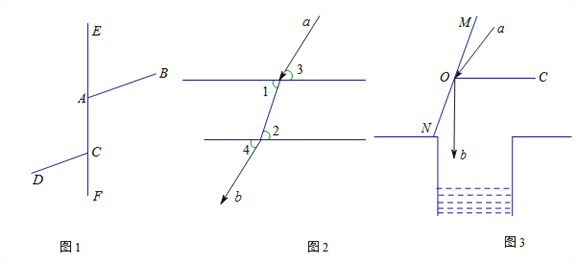
【題目】(1)光線從空氣中射入水中會產生折射現象,同時光線從水中射入空氣中也會產生折射現象,如圖1,光線a從空氣中射入水中,再從水中射入空氣中,形成光線b,根據光學知識有∠1=∠2,∠3=∠4,請判斷光線a與光線b是否平行,并說明理由;
(2)光線照射到鏡面會產生反射現象,由光學知識,入射光線與鏡面的夾角等于反射光線與鏡面的夾角,如圖2有一口井,已知入射光線a與水平線OC的夾角為40°,問如何放置平面鏡MN,可使反射光線b正好垂直照射到井底?(即求MN與水平線OC所夾的銳角);
(3)如圖3,直線EF上有兩點A、C,分別引兩條射線AB、CD.∠BAF=110°,∠DCF=60°,射線AB、CD分別繞點A、點C以1度/秒和3度/秒的速度同時順時針轉動,設時間為t秒,在射線CD轉動 一周的時間內,是否存在某時刻,使得CD與AB平行?若存在,求出所有滿足條件的時間t.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個邊長分別為a、b、c的直角三角形和一個兩條直角邊都是c的直角三角形拼成圖1。
探索發現:試用不同的方法計算圖1的面積,你能發現a、b、c間有什么數量關系?
嘗試應用:如圖2,在直角三角形ABC中,∠ACB=90°,三邊分別為a、b、c,
①若b-a=2,c=10,求此三角形的周長及面積。
②若b=12,a、c均為整數,試求出所有滿足條件的a、c的值。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+3與x軸相交于點A(﹣1,0)、B(3,0),與y軸相交于點C,點P為線段OB上的動點(不與O、B重合),過點P垂直于x軸的直線與拋物線及線段BC分別交于點E、F,點D在y軸正半軸上,OD=2,連接DE、OF.
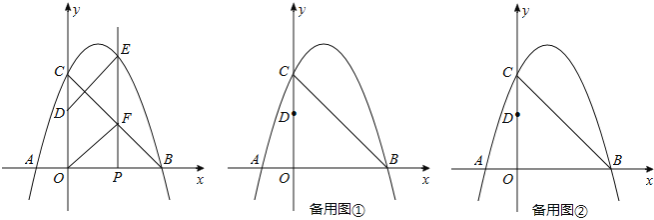
(1)求拋物線的解析式;
(2)當四邊形ODEF是平行四邊形時,求點P的坐標;
(3)過點A的直線將(2)中的平行四邊形ODEF分成面積相等的兩部分,求這條直線的解析式.(不必說明平分平行四邊形面積的理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)化簡:﹣3(x2+2xy)+6(x2﹣xy)
(2)先化簡,再求代數式的值:2(x2y+xy2)﹣2(x2y﹣2)﹣(xy2+2),其中x=2016,y=﹣1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com